Sum of the Number of Triangles

　

We are given a rectangular region in the coordinate plane with the origin $O$ at the lower left and the point at coordinates $(W,H)$ at the upper right. Consider a collection of points in this region that contains at least three points whose $x$-coordinates and $y$-coordinates are both integers. Let $N$ be the number of combinations of all such point clusters. When each collection of points is represented by $D_1, D_2,...,D_N$, consider a triangle whose vertices are the points contained in $D_1, D2,...,D_N$.

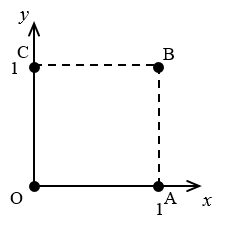
For example, as shown in the figure, when $W=H=1$, there are five groups of points {O,A,B}, {O,A,C}, {O,B,C}, {A,B,C}, and {O,A,B,C} that contain three or more of the points O(0,0), A(1,0), B(1,1), and C(0,1). In this example, the triangles contained in each of the point clusters are as follows.

• The only triangle contained in $\{O,A,B\}$ is $OAB$.
• The only triangle contained in $\{O,A,C\}$ is $OAC$.
• The only triangle contained in $\{O,B,C\}$ is $OBC$.
• The only triangle contained in $\{A,B,C\}$ is $ABC$.
• There are four triangles in $\{O,A,B,C\}$: $OAB$, $OAC$, $OBC$, $ABC$.

As you can see from this example, the same triangle may be contained in more than one set of points. For example, triangle $OAB$ is contained in both the point set $\{O,A,B\}$ and $\{O,A,B,C\}$.

$W$ and $H$ are given. Let $t_1, t_2, ..., t_N$ be the number of triangles whose vertices are points in each of the point groups $D_1, D_2, ..., D_N$. Write a program to calculate the sum of the number of triangles $t_1+t_2+...+t_N$.

Input

The input is given in the following form.

$W$ $H$

$W$ and $H$ ($1 \leq W,H \leq 1,000$) are given in a line.

Output

Output the sum of the number of triangles in each set of points. Output the remainder divided by 1,000,000,007.

Sample Input and Output

Sample Input 1

1 1

Sample Output 1

8

Sample Input 2

1 2

Sample Output 2

144

Sample Input 3

100 100

Sample Output 3

879128399

---