Warehouse Robot

Aizu Transport is developing a warehouse guard robot. In our warehouse, points in the warehouse are managed by coordinates (x,y) as shown in the floor plan below. In the warehouse, shelves with square bottoms are arranged in a regular pattern to facilitate the management of cargo. If we represent the positions of the southwest and northeast corners of the shelves by pairs of coordinates of points in the warehouse, the shelves are (0,0) and (1,1), (2,0) and (3,1), ..., (0,2) and (1,3), (2,2) and (3,3), ..., and so on, from one end of the warehouse to the other, they are placed in such a way that they occupy a square area represented by (2i,2j) and (2i+1,2j+1) using zero or more integers i and j.

The warehouseman robot can move freely when there are no shelves. It cannot pass through the area where shelves are placed, but it can pass over the boundary of the shelf area because of its small size. For example, to go from point (0,0) to point (4,3) in the shortest distance, you can move as follows.

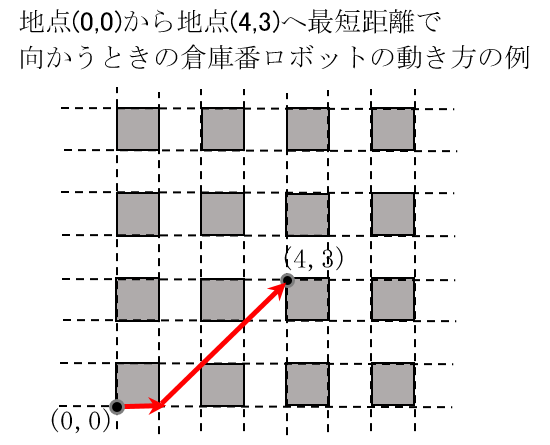
You, the warehouseman robot development department, are planning to add a function to the robot to calculate the shortest distance to the target point.

Given the point where the warehouse guard robot is currently located and the target point, write a program that outputs the shortest distance that the robot will travel to reach the target point.  

Input

The input is given in the following form.

$x_0$ $y_0$ $x_1$ $y_1$

In one line, the coordinates $x_0$,$y_0$ ($0 \leq x_0,y_0 \leq 300$) of the point where the warehouse guard robot is currently located and the coordinates $x_1$,$y_1$ ($0 \leq x_1,y_1 \leq 300$) of the target point are all given as integers. The warehouse can be thought of as a rectangle of such a size that all points with the given coordinates exist. The coordinates of the point where the robot is currently located and the target point are different ($x_0 \ne x_1$ or $y_0 \ne y_1$).

Output

Output the shortest distance for the robot to reach the target point as a real number on one line. The error must not exceed plus or minus 0.00001.

Sample Input and Output

Sample Input 1

0 0 4 3

Sample Output 1

5.24264069

Sample Input 2

7 1 1 6

Sample Output 2

7.89292223

Sample Input 3

0 2 5 2

Sample Output 3

5

 

---