Slot Machines

Aizu Industry has developed a new slot machine. This slot machine displays $W$ numbers horizontally and $H$ numbers vertically from 0 to 9. An example of the numbers displayed where $W=5$ and $H=3$ is shown in Figure 1.

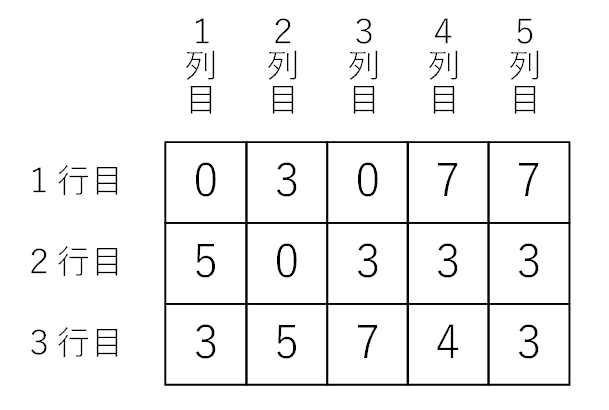
Figure 1: Example of numbers displayed on a slot machine ($W=5, H=3$)

In this slot machine, you get points according to the numbers displayed. The score is calculated as follows: when a specific same number appears in all the rows from column 1 to column $W$ (regardless of whether the rows match), you can get the score (that number) by connecting the numbers with a line to form a single broken line. If you can make multiple lines with different shapes, the sum of the scores of all the lines will be the score you get from the slot machine. If you can't make a single broken line, your score will be zero.

Let's consider the scores obtained by the numbers displayed in Figure 1 in Figure 2.

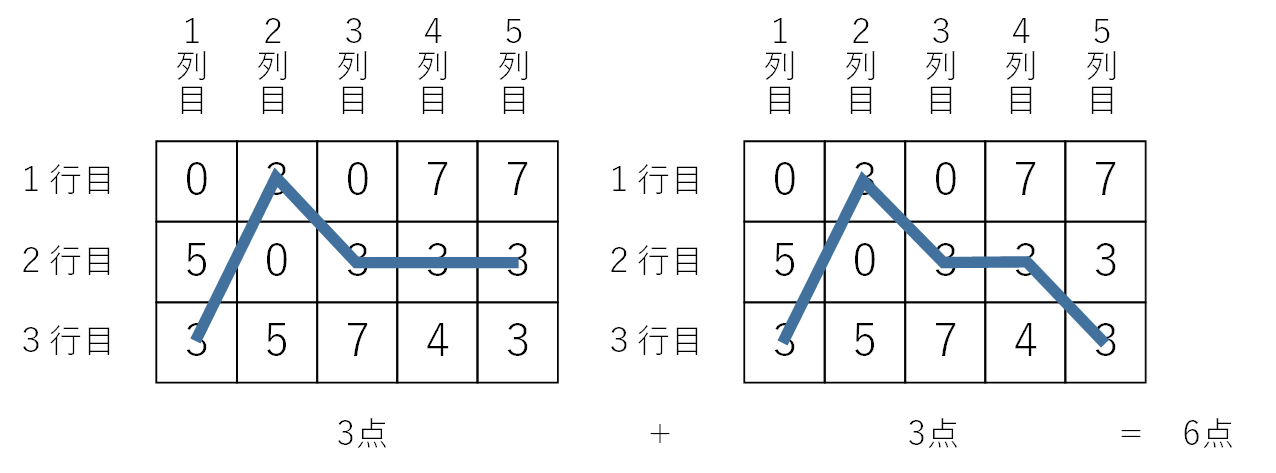
Figure 2: Example of calculating the score of a slot machine

In the example of Figure 1, since 3 appears in every row, a polyline can be formed by connecting 3. The score for each line is 3 points, so the total score for the slot machine is 6 points.

Write a program that reads the numbers shown in the slot machine and finds the score obtained.  

Input

The input is given in the following format.

$W$ $H$
$row_1$
$row_2$
 :
$row_H$

In the first row, the number of numbers in the horizontal direction $W$ ($1 \leq W \leq 1,000$), and the number of numbers in the vertical direction $H$ ($1 \leq H \leq 1,000$) are given. In the following $H$ rows, the $row_i$ of $W$ numbers to be displayed in row $i$ are given, where $row_i$ is a sequence of numbers from 0 to 9 with length $W$.

Output

Output the obtained score in a line. Print the remainder divided by 998,244,353.

Sample Input and Output

Sample Input 1

5 3
03077
50333
35743

Sample Output 1

6

Sample Input 2

4 4
3351
5335
3573
7350

Sample Output 2

28

In Sample Input 2, there are 6 lines in which 3 appears in any column, and 2 lines in which 5 appears in any column. Therefore, the score is 3 x 6 + 5 x 2 = 28.

Sample Input 3

12 5
999999999999
999999999999
999999999999
999999999999
999999999999

Sample Output 3

200776919

 

---