The Shortest Path on the Spider's Web
PCK is observing miniature spiders living in Mount Iimoriyama for his free research during the summer vacation. As shown in Figure (a), a spider's web consists of $N$ line segments evenly aligned radially from the center and $M$ concentric regular $N$ polygonal frames with vertices on these line segments. The distance between a concentric polygon and one of its outer concentric polygons, measured along a radial line segment, is 1 cm. The distance from the center of the concentric polygon to the vertex of the innermost concentric polygon is also 1 cm, but there is no line segment in between. The figure shows a nest with $N$ = 8 and $M$ = 4. The concentric polygons are numbered from 1 to $M$ in order of proximity to the center, and each radial segment is numbered from 0 to $N$ - 1, $j$. The coordinates of the intersection of the concentric polygon $i$ and the radial segment $j$ are represented by ($i$, $j$).
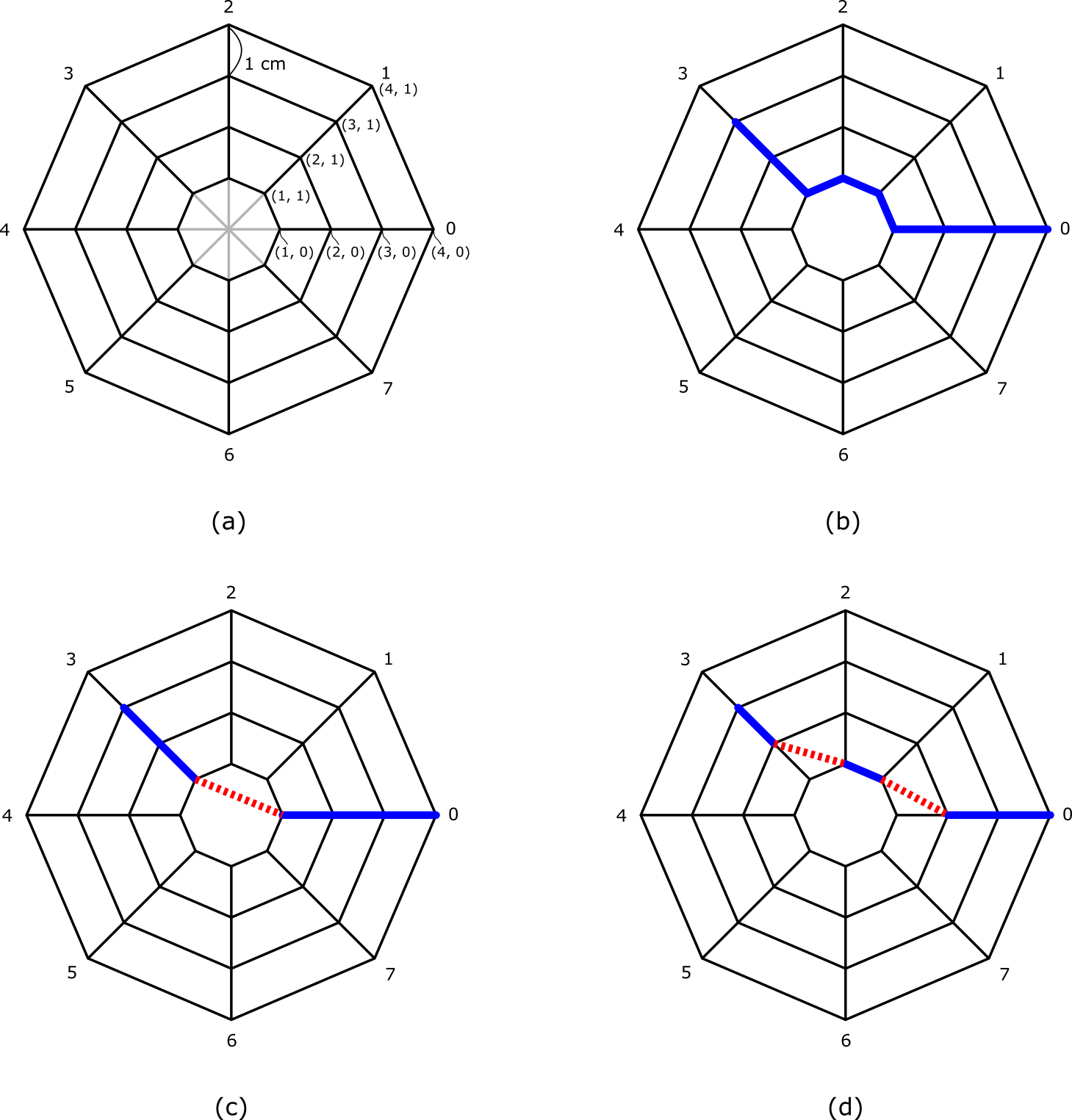
The spider can move between intersections by following the line segments that make up its web, and when its prey is caught in the web, it will move from the intersection at its current location to the intersection at its destination in the shortest possible travel distance. For example, Figure (b) shows the travel path from the current location (3, 3) to the destination (4, 0).
As a result of his research, PCK has discovered a special ability of the spider. While moving from its current location to its destination, the spider can generate up to $K$ new line segments (shown as dotted lines in the figure above) that connect intersection points and do not intersect the line segments that make up its web. For example, Figure (c) shows the path from the current location (3, 3) to the destination (4, 0) with one new line segment from the intersection point (1, 3) to the intersection point (1, 0). Figure (d) shows the path from the current location (3, 3) to the destination (4, 0), including a new line segment from the intersection (2, 3) to the intersection (1, 2) and a new line segment from the intersection (1, 1) to the intersection (2, 0).
You are given information about the size of the nest, the current location, and destination of the spider, and the maximum number of times a new line segment can be generated. Create a program to find the shortest distance (in cm) for the spider to travel from its current location to its destination.
Input
Input is given in the following format.
$N$ $M$ $K$ $r_s$ $p_s$ $r_g$ $p_g$
The first line gives the number of radial line segments $N$ ($4 \leq N \leq 20$), the number of polygons $M$ ($2 \leq M \leq 20$), and the number of times a new line segment can be generated $K$ ($0 \leq K \leq 10$). In the second line, two integers $r_s$ and $p_s$ ($1 \leq r_s \leq M$ and $0 \leq p_s < N$) are given to represent the coordinates of the spider's current location ($r_s$, $p_s$). In the third line, two integers $r_g$, $p_g$ ($1 \leq r_g \leq M$ and $0 \leq p_g < N$) are given to represent the coordinates of the spider's destination ($r_g$, $p_g$). The coordinates of the current location are different from the coordinates of the destination ($r_s \ne r_g$ or $p_s \ne p_g$).
Output
Output the shortest distance as a real number on one line. However, the error must not exceed plus or minus 0.00001.
Sample Input and Output
Sample Input 1
8 4 0 3 3 4 0
Sample Output 1
7.29610059
Sample Input 2
8 4 1 3 3 4 0
Sample Output 2
6.84775907
Sample Input 3
8 4 2 3 3 4 0
Sample Output 3
6.71261838