Jigsaw Puzzles for Computers
Ordinary Jigsaw puzzles are solved with visual hints; players solve a puzzle with the picture which the puzzle shows on finish, and the diverse patterns of pieces. Such Jigsaw puzzles may be suitable for human players, because they require abilities of pattern recognition and imagination.
On the other hand, "Jigsaw puzzles" described below may be just the things for simple-minded computers.
As shown in Figure 1,
a puzzle is composed of nine square pieces, and each of the four edges
of a piece is labeled with one of the following eight symbols:
"R", "G", "B", "W", "r", "g", "b", and "w".
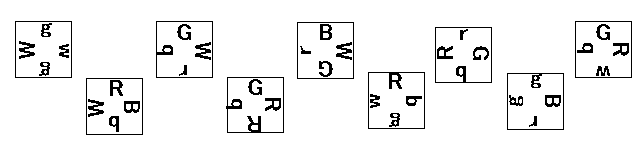 |
| Figure 1: The nine pieces of a puzzle |
In a completed puzzle, the nine pieces are arranged in a 3 x 3 grid,
and each of the 12 pairs of edges facing each other
must be labeled with one of the
following four combinations of symbols:
"R" with "r", "G" with "g",
"B" with "b", and "W" with "w".
For example, an edge labeled "R" can only face an edge with "r".
Figure 2 is an example of a completed state of a puzzle.
In the figure, edges under this restriction are indicated by shadowing their labels.
The player can freely move and rotate the pieces, but cannot turn them over.
There are no symbols on the reverse side of a piece !
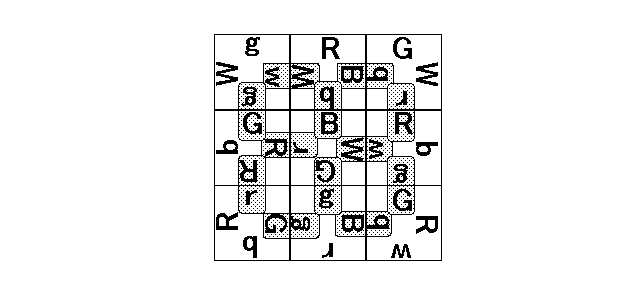 |
| Figure 2: A completed puzzle example |
Each piece is represented by a sequence of the four symbols on the piece, starting with the symbol of the top edge, followed by the symbols of the right edge, the bottom edge, and the left edge. For example, gwgW represents the leftmost piece in Figure 1. Note that the same piece can be represented as wgWg, gWgw or Wgwg since you can rotate it in 90, 180 or 270 degrees.
The mission for you is to create a program which counts the number of solutions. It is needless to say that these numbers must be multiples of four, because, as shown in Figure 3, a configuration created by rotating a solution in 90, 180 or 270 degrees is also a solution.
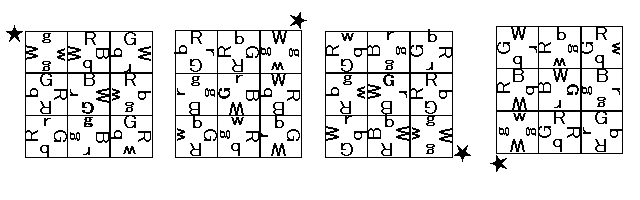 |
| Figure 3: Four obvious variations for a completed puzzle |
A term "rotationally equal" is defined; if two different pieces are identical when one piece is rotated (in 90, 180 or 270 degrees), they are rotationally equal. For example, WgWr and WrWg are rotationally equal.
Another term "rotationally symmetric" is defined; if a piece is
rotationally equal to itself, it is rotationally symmetric.
For example, a piece gWgW is rotationally symmetric.
Given puzzles satisfy the following three conditions:
- There is no identical pair of pieces in a puzzle.
- There is no rotationally equal pair of pieces in a puzzle.
- There is no rotationally symmetric piece in a puzzle.
Input
The input consists of multiple puzzles.
N
Puzzle1
Puzzle2
. . .
PuzzleN
N is the number of puzzles. Each Puzzlei
gives a puzzle with a single line
of 44 characters, consisting of four-character representations of the nine
pieces of the puzzle, separated by a space character.
For example, the following line represents the puzzle
in Figure 1.
gwgW RBbW GWrb GRRb BWGr Rbgw rGbR gBrg GRwb
Output
For each Puzzlei , the number of its solutions should be the output, each in a separate line.
Sample Input
6 WwRR wwrg RRGb rGBG RGrb RrRg RGrg rgBB Wrgr RrGb WWGR rGgb Wbrg wgBb GgBg WbBG Wwwg WWGG RBbr Wrbr wGGG wggR WgGR WBWb WRgB wBgG WBgG wBrg rGgb WRrB WWbw wRRB RbbB WRrb wrbb WgrG WrwB WWww wRRB WGGb Wbbg WBgG WrbG Wrww RBgg WWgg RBrr Rggr RGBg Wbgr WGbg WBbr WGWB GGGg
Output for the Sample Input:
40 8 32 4 12 0