Problem H: Inherit the Spheres

In the year 2xxx, an expedition team landing on a planet found strange objects made by an ancient species living on that planet. They are transparent boxes containing opaque solid spheres (Figure 1). There are also many lithographs which seem to contain positions and radiuses of spheres.

Figure 1: A strange object

Initially their objective was unknown, but Professor Zambendorf found the cross section formed by a horizontal plane plays an important role. For example, the cross section of an object changes as in Figure 2 by sliding the plane from bottom to top.

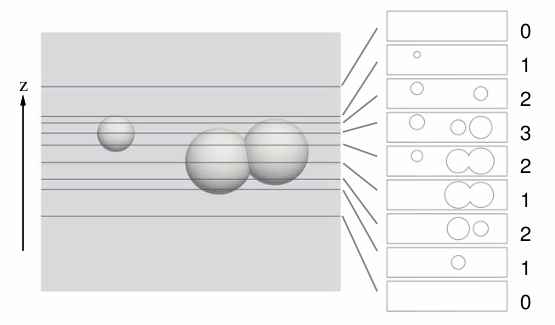
Figure 2: Cross sections at different positions

He eventually found that some information is expressed by the transition of the number of connected figures in the cross section, where each connected figure is a union of discs intersecting or touching each other, and each disc is a cross section of the corresponding solid sphere. For instance, in Figure 2, whose geometry is described in the first sample dataset later, the number of connected figures changes as 0, 1, 2, 1, 2, 3, 2, 1, and 0, at z = 0.0000, 162.0000, 167.0000, 173.0004, 185.0000, 191.9996, 198.0000, 203.0000, and 205.0000, respectively. By assigning 1 for increment and 0 for decrement, the transitions of this sequence can be expressed by an 8-bit binary number 11011000.

For helping further analysis, write a program to determine the transitions when sliding the horizontal plane from bottom (z = 0) to top (z = 36000).

Input

The input consists of a series of datasets. Each dataset begins with a line containing a positive integer, which indicates the number of spheres N in the dataset. It is followed by N lines describing the centers and radiuses of the spheres. Each of the N lines has four positive integers X_i, Y_i, Z_i, and R_i (i = 1, . . . , N) describing the center and the radius of the i-th sphere, respectively.

You may assume 1 ≤ N ≤ 100, 1 ≤ R_i ≤ 2000, 0 < X_i - R_i < X_i + R_i < 4000, 0 < Y_i - R_i < Y_i + R_i < 16000, and 0 < Z_i - R_i < Z_i + R_i < 36000. Each solid sphere is defined as the set of all points (x, y, z) satisfying (x - X_i)² + (y - Y_i)² + (z - Z_i)² ≤ R_i².

A sphere may contain other spheres. No two spheres are mutually tangent. Every Z_i ± R_i and minimum/maximum z coordinates of a circle formed by the intersection of any two spheres differ from each other by at least 0.01.

The end of the input is indicated by a line with one zero.

Output

For each dataset, your program should output two lines. The first line should contain an integer M indicating the number of transitions. The second line should contain an M-bit binary number that expresses the transitions of the number of connected figures as specified above.

Sample Input

3
95 20 180 18
125 20 185 18
40 27 195 10
1
5 5 5 4
2
5 5 5 4
5 5 5 3
2
5 5 5 4
5 7 5 3
16
2338 3465 29034 710
1571 14389 25019 842
1706 8015 11324 1155
1899 4359 33815 888
2160 10364 20511 1264
2048 8835 23706 1906
2598 13041 23679 618
1613 11112 8003 1125
1777 4754 25986 929
2707 9945 11458 617
1153 10358 4305 755
2462 8450 21838 934
1822 11539 10025 1639
1473 11939 12924 638
1388 8519 18653 834
2239 7384 32729 862
0

Output for the Sample Input

8
11011000
2
10
2
10
2
10
28
1011100100110101101000101100

---