Fair Chocolate-Cutting
You are given a flat piece of chocolate of convex polygon shape. You are to cut it into two pieces of precisely the same amount with a straight knife.
Write a program that computes, for a given convex polygon, the maximum and minimum lengths of the line segments that divide the polygon into two equal areas.
The figures below correspond to first two sample inputs. Two dashed lines in each of them correspond to the equal-area cuts of minimum and maximum lengths.
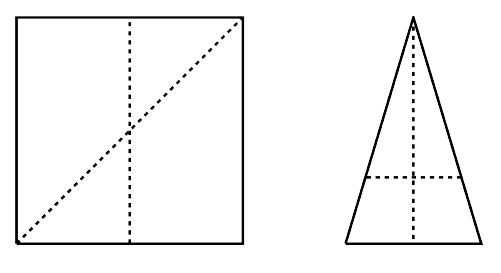
Figure F.1. Sample Chocolate Pieces and Cut Lines
Input
The input consists of a single test case of the following format.
$n$ $x_1$ $y_1$ ... $x_n$ $y_n$
The first line has an integer $n$, which is the number of vertices of the given polygon. Here, $n$ is between 3 and 5000, inclusive. Each of the following $n$ lines has two integers $x_i$ and $y_i$, which give the coordinates ($x_i, y_i$) of the $i$-th vertex of the polygon, in counterclockwise order. Both $x_i$ and $y_i$ are between 0 and 100 000, inclusive.
The polygon is guaranteed to be simple and convex. In other words, no two edges of the polygon intersect each other and interior angles at all of its vertices are less than $180^\circ$.
Output
Two lines should be output. The first line should have the minimum length of a straight line segment that partitions the polygon into two parts of the equal area. The second line should have the maximum length of such a line segment. The answer will be considered as correct if the values output have an absolute or relative error less than $10^{-6}$.
Sample Input 1
4 0 0 10 0 10 10 0 10
Sample Output 1
10 14.142135623730950488
Sample Input 2
3 0 0 6 0 3 10
Sample Output 2
4.2426406871192851464 10.0
Sample Input 3
5 0 0 99999 20000 100000 70000 33344 63344 1 50000
Sample Output 3
54475.580091580027976 120182.57592539864775
Sample Input 4
6 100 350 101 349 6400 3440 6400 3441 1200 7250 1199 7249
Sample Output 4
4559.2050019027964982 6216.7174287968524227