Estimating the Flood Risk

Mr. Boat is the owner of a vast extent of land. As many typhoons have struck Japan this year, he became concerned of flood risk of his estate and he wants to know the average altitude of his land. The land is too vast to measure the altitude at many spots. As no steep slopes are in the estate, he thought that it would be enough to measure the altitudes at only a limited number of sites and then approximate the altitudes of the rest based on them.

Multiple approximations might be possible based on the same measurement results, in which case he wants to know the worst case, that is, one giving the lowest average altitude.

Mr. Boat’s estate, which has a rectangular shape, is divided into grid-aligned rectangular areas of the same size. Altitude measurements have been carried out in some of these areas, and the measurement results are now at hand. The altitudes of the remaining areas are to be approximated on the assumption that altitudes of two adjoining areas sharing an edge differ at most 1.

In the first sample given below, the land is divided into 5 × 4 areas. The altitudes of the areas at (1, 1) and (5, 4) are measured 10 and 3, respectively. In this case, the altitudes of all the areas are uniquely determined on the assumption that altitudes of adjoining areas differ at most 1.

In the second sample, there are multiple possibilities, among which one that gives the lowest average altitude should be considered.

In the third sample, no altitude assignments satisfy the assumption on altitude differences.

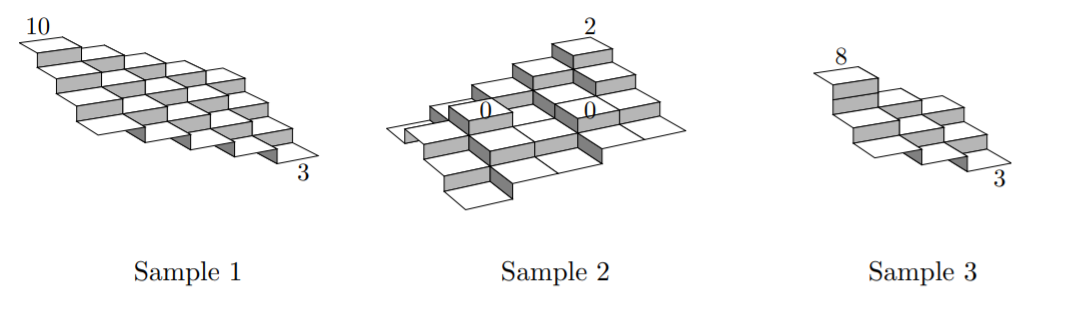
Your job is to write a program that approximates the average altitude of his estate. To be precise, the program should compute the total of approximated and measured altitudes of all the mesh-divided areas. If two or more different approximations are possible, the program should compute the total with the severest approximation, that is, one giving the lowest total of the altitudes.

Input

The input consists of a single test case of the following format.

$w$ $d$ $n$
$x_1$ $y_1$ $z_1$
.
.
.
$x_n$ $y_n$ $z_n$

Here, $w$, $d$, and $n$ are integers between $1$ and $50$, inclusive. $w$ and $d$ are the numbers of areas in the two sides of the land. $n$ is the number of areas where altitudes are measured. The $i$-th line of the following $n$ lines contains three integers, $x_i$, $y_i$, and $z_i$ satisfying $1 \leq x_i \leq w$, $1 \leq y_i \leq d$, and $−100 \leq z_i \leq 100$. They mean that the altitude of the area at $(x_i , y_i)$ was measured to be $z_i$. At most one measurement result is given for the same area, i.e., for $i \ne j$, $(x_i, y_i) \ne (x_j , y_j)$.

Output

If all the unmeasured areas can be assigned their altitudes without any conflicts with the measured altitudes assuming that two adjoining areas have the altitude difference of at most 1, output an integer that is the total of the measured or approximated altitudes of all the areas. If more than one such altitude assignment is possible, output the minimum altitude total among the possible assignments.

If no altitude assignments satisfy the altitude difference assumption, output No.

Sample Input 1

5 4 2
1 1 10
5 4 3

Sample Output 1

130

Sample Input 2

5 4 3
2 2 0
4 3 0
5 1 2

Sample Output 2

-14

Sample Input 3

3 3 2
1 1 8
3 3 3

Sample Output 3

No

Sample Input 4

2 2 1
1 1 -100

Sample Output 4

-404

---