Twin Trees Bros.

To meet the demand of ICPC (International Cacao Plantation Consortium), you have to check whether two given trees are twins or not.

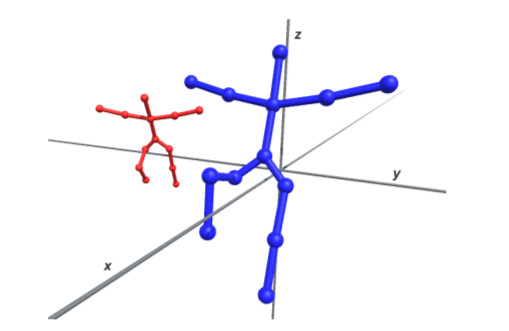
Example of two trees in the three-dimensional space.

The term tree in the graph theory means a connected graph where the number of edges is one less than the number of nodes. ICPC, in addition, gives three-dimensional grid points as the locations of the tree nodes. Their definition of two trees being twins is that, there exists a geometric transformation function which gives a one-to-one mapping of all the nodes of one tree to the nodes of the other such that for each edge of one tree, there exists an edge in the other tree connecting the corresponding nodes. The geometric transformation should be a combination of the following transformations:

• translations, in which coordinate values are added with some constants,
• uniform scaling with positive scale factors, in which all three coordinate values are multiplied by the same positive constant, and
• rotations of any amounts around either $x$-, $y$-, and $z$-axes.

Note that two trees can be twins in more than one way, that is, with different correspondences of nodes.

Write a program that decides whether two trees are twins or not and outputs the number of different node correspondences.

Hereinafter, transformations will be described in the right-handed $xyz$-coordinate system.

Trees in the sample inputs 1 through 4 are shown in the following figures. The numbers in the figures are the node numbers defined below.

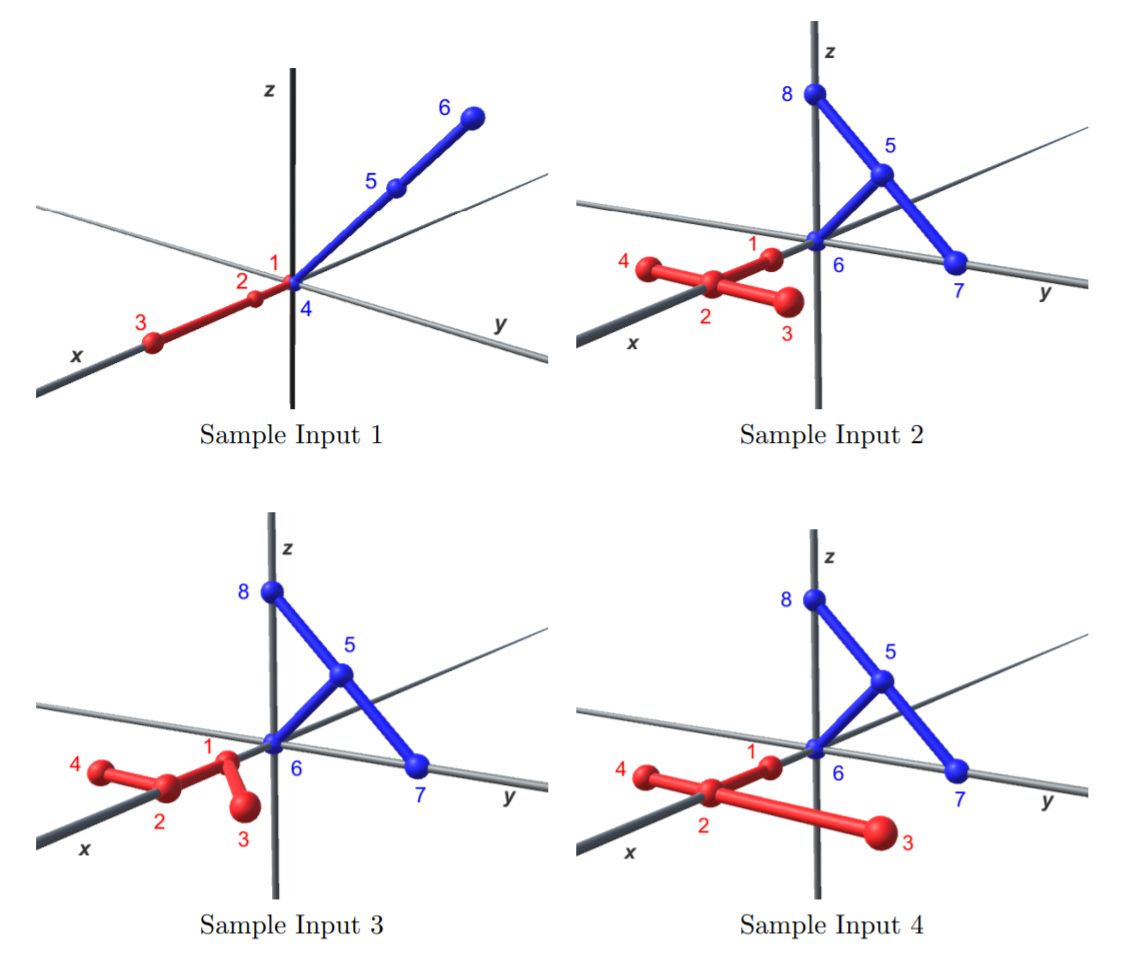
For the sample input 1, each node of the red tree is mapped to the corresponding node of the blue tree by the transformation that translates $(-3, 0, 0)$, rotates $-\pi / 2$ around the $z$-axis, rotates $\pi / 4$ around the $x$-axis, and finally scales by $\sqrt{2}$. By this mapping, nodes #1, #2, and #3 of the red tree at $(0, 0, 0)$, $(1, 0, 0)$, and $(3, 0, 0)$ correspond to nodes #6, #5, and #4 of the blue tree at $(0, 3, 3)$, $(0, 2, 2)$, and $(0, 0, 0)$, respectively. This is the only possible correspondence of the twin trees.

For the sample input 2, red nodes #1, #2, #3, and #4 can be mapped to blue nodes #6, #5, #7, and #8. Another node correspondence exists that maps nodes #1, #2, #3, and #4 to #6, #5, #8, and #7.

For the sample input 3, the two trees are not twins. There exist transformations that map nodes of one tree to distinct nodes of the other, but the edge connections do not agree.

For the sample input 4, there is no transformation that maps nodes of one tree to those of the other.

Input

The input consists of a single test case of the following format.

$n$
$x_1$ $y_1$ $z_1$
.
.
.
$x_n$ $y_n$ $z_n$
$u_1$ $v_1$
.
.
.
$u_{n−1}$ $v_{n−1}$
$x_{n+1}$ $y_{n+1}$ $z_{n+1}$
.
.
.
$x_{2n}$ $y_{2n}$ $z_{2n}$
$u_n$ $v_n$
.
.
.
$u_{2n−2}$ $v_{2n−2}$

The input describes two trees. The first line contains an integer $n$ representing the number of nodes of each tree ($3 \leq n \leq 200$). Descriptions of two trees follow.

Description of a tree consists of $n$ lines that give the vertex positions and $n - 1$ lines that show the connection relation of the vertices.

Nodes are numbered $1$ through $n$ for the first tree, and $n + 1$ through $2n$ for the second tree.

The triplet $(x_i, y_i, z_i)$ gives the coordinates of the node numbered $i$. $x_i$, $y_i$, and $z_i$ are integers in the range between $-1000$ and $1000$, inclusive. Nodes of a single tree have distinct coordinates.

The pair of integers $(u_j , v_j )$ means that an edge exists between nodes numbered $u_j$ and $v_j$ ($u_j \ne v_j$). $1 \leq u_j \leq n$ and $1 \leq v_j \leq n$ hold for $1 \leq j \leq n - 1$, and $n + 1 \leq u_j \leq 2n$ and $n + 1 \leq v_j \leq 2n$ hold for $n \leq j \leq 2n - 2$.

Output

Output the number of different node correspondences if two trees are twins. Output a zero, otherwise.

Sample Input 1

3
0 0 0
1 0 0
3 0 0
1 2
2 3
0 0 0
0 2 2
0 3 3
4 5
5 6

Sample Output 1

1

Sample Input 2

4
1 0 0
2 0 0
2 1 0
2 -1 0
1 2
2 3
2 4
0 1 1
0 0 0
0 2 0
0 0 2
5 6
5 7
5 8

Sample Output 2

2

---