Tree Generators

One of the problems in the International Parsing Contest caught your attention.

Two expressions are given as input, each representing a procedure to generate a single tree. The gen eration procedure is randomized, meaning different trees may be generated each time the procedure is performed. You are asked to count the number of trees that can possibly be generated from both of the expressions.

The syntax of an expression is as follows.

$E$ $::=$ '1' $|$ '(' $E$ $E$ ')'

A tree is generated from an expression according to the following procedure.

• The expression 1 generates a tree with a single vertex labeled 1.
• For two expressions $E_1$ and $E_2$, an expression ($E_1 E_2$) generates a tree as follows:
  • A tree $T_1$ is generated from $E_1$ with $n_1$ vertices, and $T_2$ from $E_2$ with $n_2$ vertices.
  • Then, the labels of all vertices in $T_2$ are incremented by $n_1$.
  • After that, two vertices, one from $T_1$ and the other from $T_2$, are randomly chosen. Adding an edge connecting them forms a single tree with vertices labeled 1 through ($n_1 + n_2$), which is the tree generated by ($E_1 E_2$).

For example, the expression (11) can generate only the leftmost tree in Figure D.1, while (1(11)) can generate the remaining two trees.

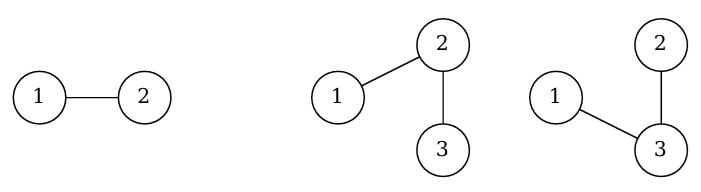
Figure D.1. Trees generated from the two expressions, (11) and (1(11))

The same tree may be generated from different expressions. The middle tree can also be generated from ((11)1).

For given two expressions of the same length, count the number of trees that can be generated from both of the expressions. Note that the trees generated from them always have the same number of vertices. Two trees are considered different if there exist two indices $i$ and $j$ such that vertices labeled $i$ and $j$ are connected by an edge in one tree but not in the other.

Input

The input consists of two lines, each containing an expression string. The two strings have the same length, between $1$ and $7 \times 10^5$, inclusive, and follow the syntax given above.

Output

Output the number of trees that can be generated from both expressions modulo 998244353.

Sample Input 1

((1(11))1)
((11)(11))

Sample Output 1

1

Sample Input 2

(1(11))
(1(11))

Sample Output 2

2

Sample Input 3

(((11)(11))((11)1))
((1(11))(1(1(11))))

Sample Output 3

3

Sample Input 4

((11)(((1(11))1)((11)1)))
(1(((11)((11)(11)))(11)))

Sample Output 4

4

For Sample Input 1, the trees that can be generated from the two expressions are shown in Figure D.2. The top six trees correspond to the first expression and the bottom four correspond to the second. Only the leftmost tree in each row can be generated from both.

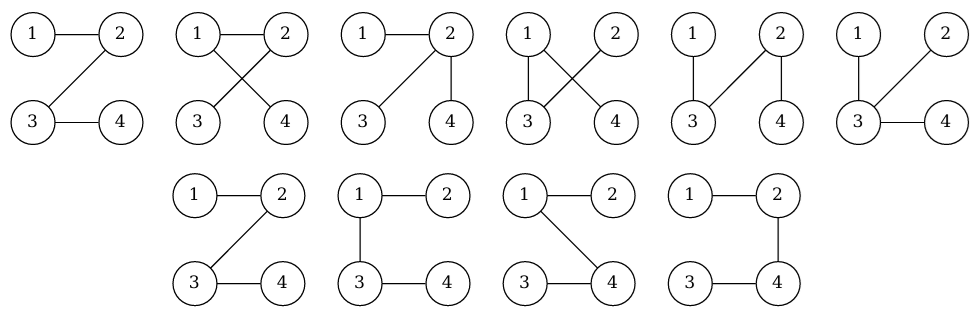
Figure D.2. Illustration of Sample Input 1

---