Complex Paper Folding

Dr. G, an authority in paper folding and one of the directors of Intercultural Consortium on Paper Crafts, believes complexity gives figures beauty. As one of his assistants, your job is to find the way to fold a paper to obtain the most complex figure. Dr. G defines the complexity of a figure by the number of vertices. With the same number of vertices, one with longer perimeter is more complex. To simplify the problem, we consider papers with convex polygon in their shapes and folding them only once. Each paper should be folded so that one of its vertices exactly lies on top of another vertex.

Write a program that, for each given convex polygon, outputs the perimeter of the most complex polygon obtained by folding it once.

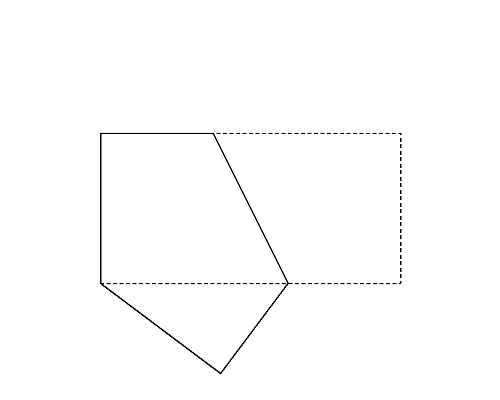
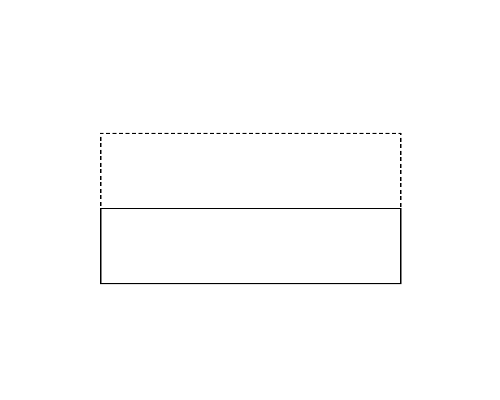
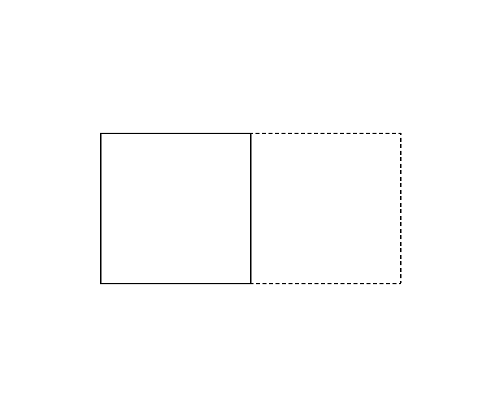
Figure 1 (left) illustrates the polygon given in the first dataset of Sample Input. This happens to be a rectangle. Folding this rectangle can yield three different polygons illustrated in the Figures 1-a to c by solid lines. For this dataset, you should answer the perimeter of the pentagon shown in Figure 1-a. Though the rectangle in Figure 1-b has longer perimeter, the number of vertices takes priority.

	(a)	(b)	(c)

Figure 1: The case of the first sample input

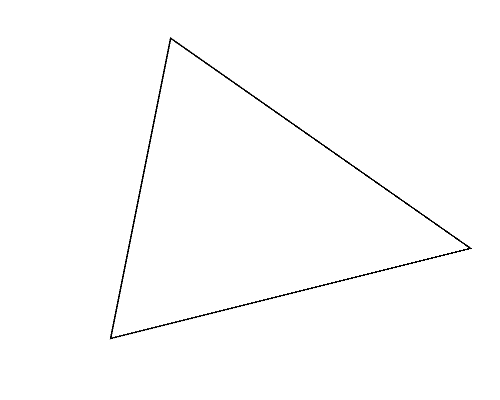
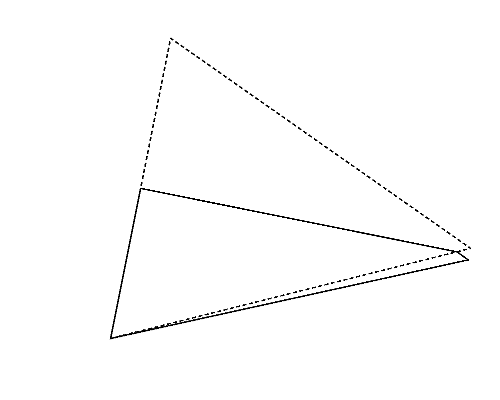
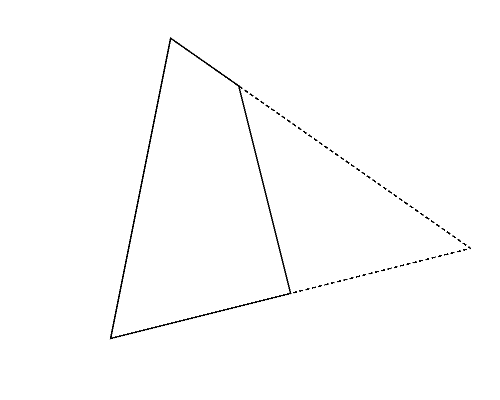
Figure 2 (left) illustrates the polygon given in the second dataset of Sample Input, which is a triangle. Whichever pair of its vertices are chosen, quadrangles are obtained as shown in Figures 2-a to c. Among these, you should answer the longest perimeter, which is that of the quadrangle shown in Figure 2-a.

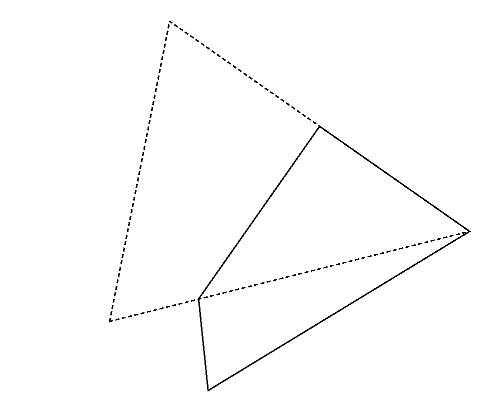	(a)	(b)	(c)

Figure 2: The case of the second sample input

Although we start with a convex polygon, folding it may result a concave polygon. Figure 3 (left) illustrates the polygon given in the third dataset in Sample Input. A concave hexagon shown in Figure 3 (right) can be obtained by folding it, which has the largest number of vertices.

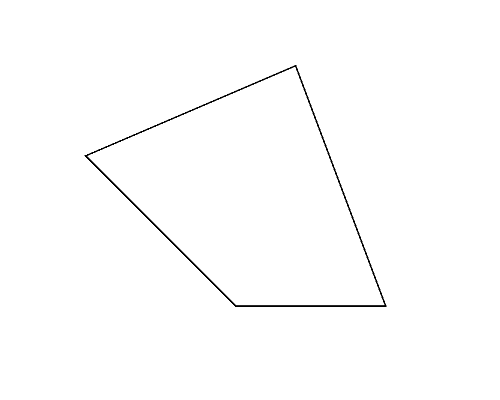
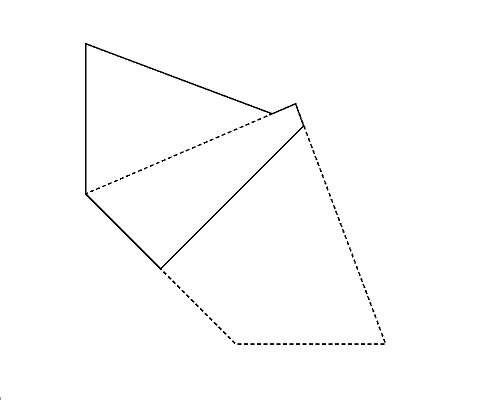
Figure 3: The case of the third sample input

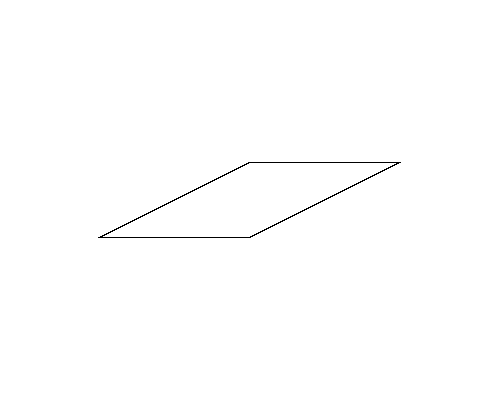
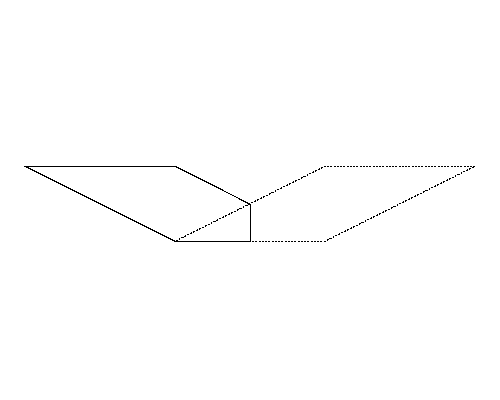
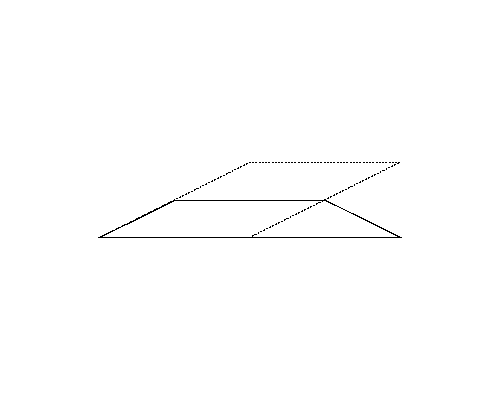
Figure 4 (left) illustrates the polygon given in the fifth dataset in Sample Input. Although the perimeter of the polygon in Figure 4-b is longer than that of the polygon in Figure 4-a, because the polygon in Figure 4-b is a quadrangle, the answer should be the perimeter of the pentagon in Figure 4-a.

	(a)	(b)

Figure 4: The case of the fifth sample input

Input

The input consists of multiple datasets, each in the following format.

n
x₁ y₁
...
x_n y_n

n is the number of vertices of the given polygon. n is a positive integer satisfying 3 ≤ n ≤ 20. (x_i, y_i) gives the coordinates of the i-th vertex. x_i and y_i are integers satisfying 0 ≤ x_i, y_i < 1000. The vertices (x₁, y₁), ..., (x_n, y_n) are given in the counterclockwise order on the xy-plane with y axis oriented upwards. You can assume that all the given polygons are convex.

All the possible polygons obtained by folding the given polygon satisfy the following conditions.

• Distance between any two vertices is greater than or equal to 0.00001.
• For any three consecutive vertices P, Q, and R, the distance between the point Q and the line passing through the points P and R is greater than or equal to 0.00001.

The end of the input is indicated by a line with a zero.

Output

For each dataset, output the perimeter of the most complex polygon obtained through folding the given polygon. The output value should not have an error greater than 0.00001. Any extra characters should not appear in the output.

Sample Input

4
0 0
10 0
10 5
0 5
3
5 0
17 3
7 10
4
0 5
5 0
10 0
7 8
4
0 0
40 0
50 5
0 5
4
0 0
10 0
20 5
10 5
7
4 0
20 0
24 1
22 10
2 10
0 6
0 4
18
728 997
117 996
14 988
1 908
0 428
2 98
6 54
30 28
106 2
746 1
979 17
997 25
998 185
999 573
999 938
995 973
970 993
910 995
6
0 40
0 30
10 0
20 0
40 70
30 70
0

Output for the Sample Input

23.090170
28.528295
23.553450
97.135255
34.270510
57.124116
3327.900180
142.111776

---