Addition on Convex Polygons

Mr. Convexman likes convex polygons very much. During his study on convex polygons, he has come up with the following elegant addition on convex polygons.

The sum of two points in the xy-plane, (x₁, y₁) and (x₂, y₂) is defined as (x₁ + x₂, y₁ + y₂). A polygon is treated as the set of all the points on its boundary and in its inside. Here, the sum of two polygons S₁ and S₂, S₁ + S₂, is defined as the set of all the points v₁ + v₂ satisfying v₁ ∈ S₁ and v₂ ∈ S₂. Sums of two convex polygons, thus defined, are always convex polygons! The multiplication of a non-negative integer and a polygon is defined inductively by 0S = {(0, 0)} and, for a positive integer k, kS = (k - 1)S + S. In this problem, line segments and points are also considered as convex polygons.

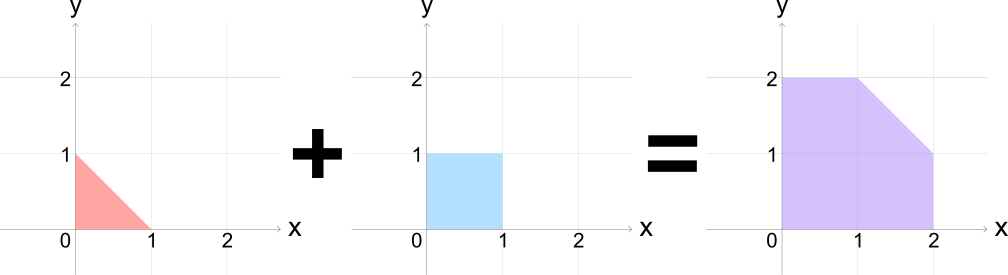
Mr. Convexman made many convex polygons based on two convex polygons P and Q to study properties of the addition, but one day, he threw away by mistake the piece of paper on which he had written down the vertex positions of the two polygons and the calculation process. What remains at hand are only the vertex positions of two convex polygons R and S that are represented as linear combinations of P and Q with non-negative integer coefficients:

R = aP + bQ, and
S = cP + dQ.

Fortunately, he remembers that the coordinates of all vertices of P and Q are integers and the coefficients a, b, c and d satisfy ad - bc = 1.

Mr. Convexman has requested you, a programmer and his friend, to make a program to recover P and Q from R and S, that is, he wants you to, for given convex polygons R and S, compute non-negative integers a, b, c, d (ad - bc = 1) and two convex polygons P and Q with vertices on integer points satisfying the above equation. The equation may have many solutions. Make a program to compute the minimum possible sum of the areas of P and Q satisfying the equation.

Input

The input consists of at most 40 datasets, each in the following format.

n m
x₁ y₁
...
x_n y_n
x'₁ y'₁
...
x'_m y'_m

n is the number of vertices of the convex polygon R, and m is that of S. n and m are integers and satisfy 3 ≤ n ≤ 1000 and 3 ≤ m ≤ 1000. (x_i, y_i) represents the coordinates of the i-th vertex of the convex polygon R and (x'_i, y'_i) represents that of S. x_i, y_i, x'_i and y'_i are integers between −10⁶ and 10⁶, inclusive. The vertices of each convex polygon are given in counterclockwise order. Three different vertices of one convex polygon do not lie on a single line.

The end of the input is indicated by a line containing two zeros.

Output

For each dataset, output a single line containing an integer representing the double of the sum of the areas of P and Q. Note that the areas are always integers when doubled because the coordinates of each vertex of P and Q are integers.

Sample Input

5 3
0 0
2 0
2 1
1 2
0 2
0 0
1 0
0 1
4 4
0 0
5 0
5 5
0 5
0 0
2 0
2 2
0 2
3 3
0 0
1 0
0 1
0 1
0 0
1 1
3 3
0 0
1 0
1 1
0 0
1 0
1 1
4 4
0 0
2 0
2 2
0 2
0 0
1 0
1 2
0 2
4 4
0 0
3 0
3 1
0 1
0 0
1 0
1 1
0 1
0 0

Output for the Sample Input

3
2
2
1
0
2

---