Web 0.5
In a forest, there lived a spider named Tim. Tim was so smart that he created a huge, well-structured web. Surprisingly, his web forms a set of equilateral and concentric N-sided polygons whose edge lengths form an arithmetic sequence.
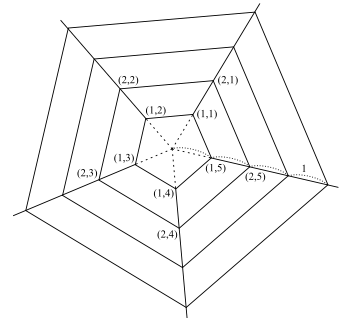
Figure 1: An example web of Tim
Corresponding vertices of the N-sided polygons lie on a straight line, each apart from neighboring ver- tices by distance 1. Neighboring vertices are connected by a thread (shown in the figure as solid lines), on which Tim can walk (you may regard Tim as a point). Radial axes are numbered from 1 to N in a rotational order, so you can denote by (r, i) the vertex on axis i and apart from the center of the web by distance r. You may consider the web as infinitely large, i.e. consisting of infinite number of N-sided polygons, since the web is so gigantic.
Tim’s web is thus marvelous, but currently has one problem: due to rainstorms, some of the threads are damaged and Tim can’t walk on those parts.
Now, a bug has been caught on the web. Thanks to the web having so organized a structure, Tim accu- rately figures out where the bug is, and heads out for that position. You, as a biologist, are interested in whether Tim is smart enough to move through the shortest possible route. To judge that, however, you need to know the length of the shortest route yourself, and thereby decided to write a program which calculates that length.
Input
The input consists of multiple test cases. Each test case begins with a line containing two integers N (3 ≤ N ≤ 100) and X (0 ≤ X ≤ 100), where N is as described above and X denotes the number of damaged threads. Next line contains four integers rS, iS, rT, and iT, meaning that Tim is starting at (rS, iS) and the bug is at (rT, iT). This line is followed by X lines, each containing four integers rA, iA, rB, and iB, meaning that a thread connecting (rA, iA) and (rB, iB) is damaged. Here (rA, iA) and (rB, iB) will be always neighboring to each other. Also, for all vertices (r, i) given above, you may assume 1 ≤ r ≤ 107 and 1 ≤ i ≤ N.
There will be at most 200 test cases. You may also assume that Tim is always able to reach where the bug is.
The input is terminated by a line containing two zeros.
Output
For each test case, print the length of the shortest route in a line. You may print any number of digits after the decimal point, but the error must not be greater than 0.01.
Sample Input
5 1 2 1 3 2 2 1 2 2 0 0
Output for the Sample Input
4.18