English text is not available in this practice contest.

イコとピコはACM博士によって開発された人工知能を搭載した双子のロボットである．今日は二人の誕生日なので，博士は二人のためにたくさんのイチゴがのったケーキを用意した．

ケーキは横幅 W ×奥行き H の長方形の形をしている． 便宜上，ケーキは上から見たとき(0,0)，(W ,0)，(W ,H )，(0,H )を頂点とする長方形になるように置かれているとする． また，二人に均等になるようにちょうど2N 個のイチゴが乗っている．

せっかくなので，博士は二人にケーキを切らせることにした． イコとピコは協力してケーキを切るため，イコが包丁の一端を辺(0,0)-(0,H )の間におき，ピコはもう一端を辺(W ,0)-(W ,H )の間において同時に下に下ろすという方法をとることにした． もちろん包丁は直線状なので，選んだ2点を通る直線でケーキは2つに分かれる．(図E-1)

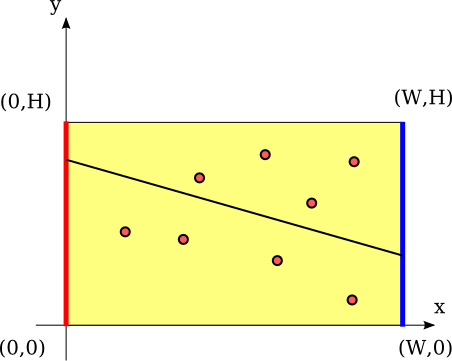
図E-1

博士は人工知能を完成させたことに満足し他の部分を適当に作ったために，二人の腕のパーツは不安定になってしまった． そのため，辺(0,0)-(0,H )(または辺(W ,0)-(W ,H ))上の狙った場所に置こうとしてもどうしてもずれてしまうのである．

二人はイチゴが好きなので，できれば N 個ずつに分けたいと考えている． そこで，N 個ずつになるように切れない場合は2点を選びなおすことにした． 2N 個のイチゴの配置によっては半分ずつに分けられなかったり，分けられたとしても，とても確率が低い場合も考えられる． このような場合に何度も2点を選びなおすのは不毛なので，まず初めに N 個ずつに分かれるように切れる確率を計算することにした．

二人の腕のパーツは不安定なので，動きを予想するのは難しい． とりあえず，二人は「包丁を置く点は辺(0,0)-(0,H )(または辺(W ,0)-(W ,H ))上に必ず乗り，置かれる確率はどの二点も等しい」という仮定を置くことにした． また，イチゴの大きさを考慮するのも面倒なので，点とみなすことにした．

これは人工知能の性能を試すいい機会である． 博士と同じ研究所に勤めているあなたに，2N 個のイチゴの位置を与えられたときに， 2人と同じ仮定を用いてイチゴが N 個ずつに分かれる確率を計算するプログラムを作成する仕事が割り当てられた．

入力は複数のデータセットからなる．入力の終わりは空白で区切られた3つのゼロからなる行によって与えられる．各データセットは1つのケーキに関する情報を表し，その形式は以下の通りである．

W H N
x₁ y₁
...
x_2N y_2N

データセットの最初の行は3つの整数 W ,H ,N からなり，それぞれケーキの横幅，奥行き，イチゴの個数/2を表す． 続く2N 行は2個の整数からなり，それぞれイチゴのx座標とy座標を表す．

それぞれの値は次の制約を満たしている．

• 1 ≤ W ,H ≤ 1,000
• 1 ≤ N ≤ 100
• 0 ≤ x_i ≤ W
• 0 ≤ y_i ≤ H

また，2つの異なるイチゴが同じ座標にあることはない．

それぞれのデータセットに対して， 2人の仮定を用いた場合にイチゴが2等分される確率を表す実数を1行に出力せよ． 答えには 10^-8 を越える誤差があってはいけない．それ以外の余計な文字を出力してはならない．

2 2 1
0 1
2 1
3 3 1
1 1
2 1
0 0 0

0.5000000000
0.1666666667