Sunny Graph

The Sun is a great heavenly body. The Sun is worshiped by various religions. Bob loves the Sun and loves any object that is similar to the Sun. He noticed that he can find the shape of the Sun in certain graphs. He calls such graphs "Sunny".

We define the property "Sunny" mathematically. A graph G=(V,E) with a vertex v \in V is called "Sunny" when there exists a subgraph G'=(V,E'), E' \subseteq E that has the following two properties. (Be careful, the set of vertices must be the same.)

1. The connected component containing v is a cycle that consists of three or more vertices.

2. Every other component has exactly two vertices.

The following picture is an example of a subgraph G'=(V,E') that has the above property.

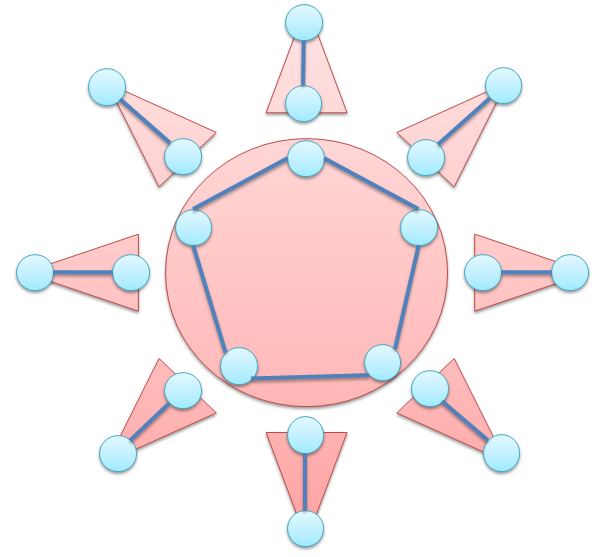
Given a simple graph (In each edge, two end points are different. Every pair of vertices has one or no edge.) G=(V,E), write a program that decides whether the given graph with the vertex 1 is "Sunny" or not.

Input

The first line contains two integers N (odd, 1 \leq N \leq 200) and M (0 \leq M \leq 20,000), separated by a single space. N is the number of the vertices and M is the number of the edges.

The following M lines describe the edges. Each line contains two integers v_i and u_i (1 \leq u_i, v_i \leq N). (u_i, v_i) indicates the edge that connects the two vertices u_i and v_i. u_i and v_i are different, and every pair (u_i,v_i) are different.

Output

Print a line containing "Yes" when the graph is "Sunny". Otherwise, print "No".

Sample Input 1

5 5
1 2
2 3
3 4
4 5
1 3

Output for the Sample Input 1

Yes

Sample Input 2

5 5
1 2
2 3
3 4
4 5
1 4

Output for the Sample Input 2

No

---