Koto Municipal Subway

Koto市営地下鉄

Koto市は，下図のように，道路が碁盤の目状である有名な街である． 南北に伸びる道と東西に伸びる道は，それぞれ1kmの間隔で並んでいる． Koto市の最も南西の交差点にあるKoto駅を (0, 0) として，そこから東に x km，北に y km 進んだ位置を (x, y) と記すこととする (0 ≤ x, y である)．

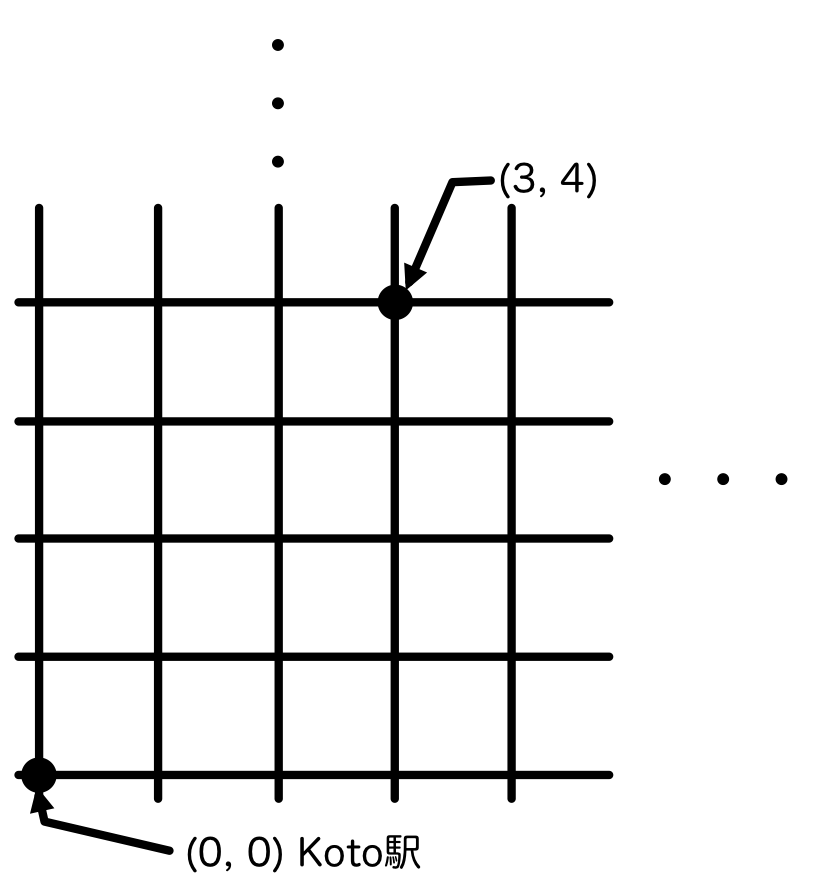
5年後に開かれるオリンピックにより観光客が増大することを見越して，市はKoto駅を始発駅とする新しい地下鉄の路線を建設することを決めた． 現在，Koto駅の次の駅として新しく建設されるShin-Koto駅までのレールを敷く計画を立てている． レールは，Koto駅からShin-Koto駅に向かってまっすぐ敷く． 従って，Shin-Koto駅の場所を (x, y) としたとき，レールの長さは， √(x² + y²) である． レールを敷くための費用は，敷いたレールの長さ分だけ必要になる． レールの長さが1.5kmのように小数であっても，費用も同じように1.5必要となる．

Shin-Koto駅の場所 (x, y) はまだ決定しておらず，以下の条件を満たす場所にする予定である．

• 交差点である．つまり， x と y がそれぞれ整数である．
• Koto駅から道路に沿って歩いた最短距離が，ちょうど D である．つまり， x + y = D を満たす．

上の2つの条件を満たす中で，市が定めるレールの予算 E とレールの費用とのずれ | √(x² + y²) - E | が最小となるようにShin-Koto駅の場所を選ぶ． ここで |A| は， A の絶対値を表す． あなたの仕事は，上記のようにShin-Koto駅を建設したときの，レールを敷くための費用と予算とのずれを出力するプログラムを作成することである．

Input

入力は，複数のデータセットから構成され，1つの入力に含まれるデータセットの数は100以下である． 各データセットの形式は次の通りである．

D E

D (1 ≤ D ≤ 100)は，Koto駅からShin-Koto駅まで道路に沿って歩いたときの最短距離を表す整数である． E (1 ≤ E ≤ 100)は，レール建設のための予算を表す整数である．

入力の終わりは，空白で区切られた2つのゼロからなる行によって示される．

Output

各データセットに対して，問題の条件を満たすようにレールを敷いたときの費用と予算とのずれを1行で出力せよ． 答えには 10^-3 を越える絶対誤差があってはならない． 各行の終わりに改行を出力しなかった場合や，不必要な文字を出力した場合，誤答と判断されてしまうため，注意すること．

Sample Input

2 1
7 5
7 6
7 7
76 5
8 41
0 0

Output for Sample Input

0.4142135624
0
0.0827625303
0
48.7401153702
33

Hint

1つ目のデータセットでは，下図のように，Koto駅から道路に沿って2km進んだ交差点がShin-Koto駅を建設する場所の候補となる．

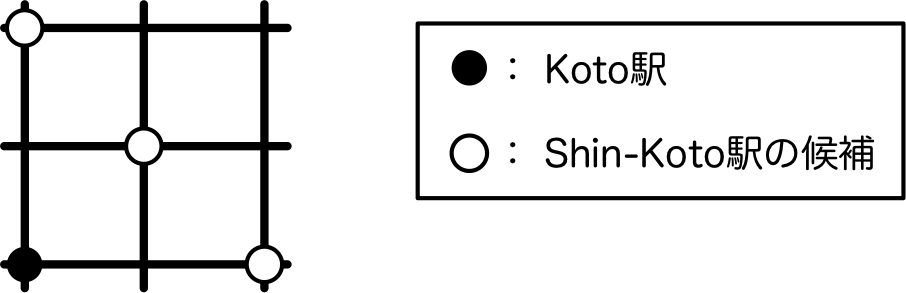
各交差点にShin-Koto駅を建設した場合の，レールを敷くための費用と予算1とのずれは次のようになる．

• (2, 0) ： | √(2² + 0²) - 1 | = 1.0
• (1, 1) ： | √(1² + 1²) - 1 | = 0.4142135623...
• (0, 2) ： | √(0² + 2²) - 1 | = 1.0

よって，費用と予算とのずれが最小になるのは， (1, 1) に建設した場合となる．

---