F - 土地相続

Problem Statement

ある $N$ 人の兄弟は親の遺産相続の話し合いをしていた． 彼らの親の残した莫大な遺産の中には広大な土地も含まれていた． その土地は南北に $H$ km, 東西に $W$ km に広がる長方形の形をしている． この土地は 1 km 四方の区画単位で管理されており， 土地の北端から $i$ 〜 $i+1$ km かつ西端から $j$ 〜 $j+1$ km の範囲にある 1 km 四方の区画を区画 $(i, j)$ と呼ぶ． （$i$, $j$ は $0 \leq i < H$, $0 \leq j < W$ を満たす整数である．） 土地の価格は区画ごとに決まっており，区画 $(i, j)$ の価格は $a_{i, j}$ で表される．

兄弟は次のように土地を分けて相続することにした．

• $N$ 人の兄弟それぞれが区画をいくつか選び相続する．
• 各兄弟が相続する土地が 1 つの長方形を成すように区画を選ばなければならない．
• $N$ 人の兄弟が相続する土地は重なってはならない．
• 誰も相続しない区画があってもよい．誰も相続しない区画は放棄される．

ある人が相続する土地の範囲に含まれる区画の価格の和をその土地の価格と呼ぶ． 兄弟は，各々が相続する土地の価格がなるべく公平になるように土地を分けたい． あなたの仕事は， $N$ 人の中で相続する土地の価格が 最も低い人の土地の価格を最大にするような土地の分け方を考えることである． そのように土地を分けた時の，相続する土地の価格が最も低い人の土地の価格を答えるプログラムを作成せよ．

Input

入力は以下のような形式で与えられる．

$H$ $W$ $N$
$a_{0,0}$ $a_{0,1}$ ... $a_{0,W-1}$
...
$a_{H-1,0}$ $a_{H-1,1}$ ... $a_{H-1,W-1}$

$H$, $W$ $(2 \leq H,W \leq 200)$ は遺産の土地の南北の長さと東西の長さをそれぞれ表す． $N$ $(2 \leq N \leq 4)$ は土地を相続する兄弟の人数を表す． $a_{i, j}$ $(0 \leq a_{i,j} \leq 10^4)$ は区画 $(i, j)$ の価格を表す．

Output

相続する土地の価格が最も低い人の土地の価格を最大にするように分けた時の， 最も低い土地の価格を 1 行で出力せよ．

Sample Input 1

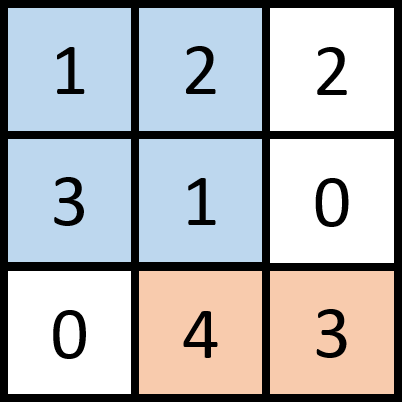
3 3 2
1 2 2
3 1 0
0 4 3

Output for the Sample Input 1

7

図のように分けるのが最適である．

Sample Input 2

3 3 2
0 1 0
1 1 1
0 1 0

Output for the Sample Input 2

1

Sample Input 3

2 5 3
8 3 0 5 6
2 5 2 5 2

Output for the Sample Input 3

11

Sample Input 4

3 3 4
3 3 4
3 3 4
3 3 4

Output for the Sample Input 4

7

Sample Input 5

4 4 4
2 2 2 2
2 1 2 1
2 2 2 2
2 1 2 1

Output for the Sample Input 5

7

---