Librarian's Work

Japanese Animal Girl Library (JAG Library) is famous for a long bookshelf. It contains $N$ books numbered from $1$ to $N$ from left to right. The weight of the $i$-th book is $w_i$.

One day, naughty Fox Jiro shuffled the order of the books on the shelf! The order has become a permutation $b_1, ..., b_N$ from left to right. Fox Hanako, a librarian of JAG Library, must restore the original order. She can rearrange a permutation of books $p_1, ..., p_N$ by performing either operation A or operation B described below, with arbitrary two integers $l$ and $r$ such that $1 \leq l < r \leq N$ holds.

Operation A:

• A-1. Remove $p_l$ from the shelf.
• A-2. Shift books between $p_{l+1}$ and $p_r$ to $left$.
• A-3. Insert $p_l$ into the $right$ of $p_r$.

Operation B:

• B-1. Remove $p_r$ from the shelf.
• B-2. Shift books between $p_l$ and $p_{r-1}$ to $right$.
• B-3. Insert $p_r$ into the $left$ of $p_l$.

This picture illustrates the orders of the books before and after applying operation A and B for $p = (3,1,4,5,2,6), l = 2, r = 5$.

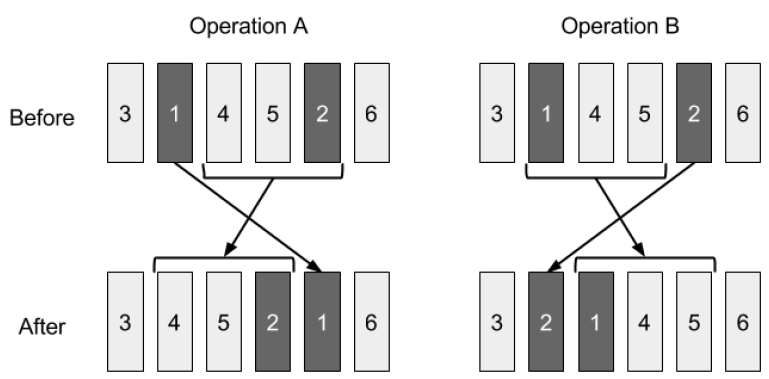
Since the books are heavy, operation A needs $\sum_{i=l+1}^r w_{p_i} + C \times (r-l) \times w_{p_l}$ units of labor and operation B needs $\sum_{i=l}^{r-1} w_{p_i} + C \times (r-l) \times w_{p_r}$ units of labor, where $C$ is a given constant positive integer.

Hanako must restore the initial order from $b_i, ..., b_N$ by performing these operations repeatedly. Find the minimum sum of labor to achieve it.

Input

The input consists of a single test case formatted as follows.

$N$ $C$
$b_1$ $w_{b_1}$
:
$b_N$ $w_{b_N}$

The first line conists of two integers $N$ and $C$ ($1 \leq N \leq 10^5, 1 \leq C \leq 100$). The ($i+1$)-th line consists of two integers $b_i$ and $w_{b_i}$ ($1 \leq b_i \leq N, 1 \leq w_{b_i} \leq 10^5$). The sequence ($b_1, ..., b_N$) is a permutation of ($1, ..., N$).

Output

Print the minimum sum of labor in one line.

Sample Input 1

3 2
2 3
3 4
1 2

Output for Sample Input 1

15

Performing operation B with $l = 1, r = 3$, i.e. removing book 1 then inserting it into the left of book 2 is an optimal solution. It costs $(3+4)+2\times2\times2=15$ units of labor.

Sample Input 2

3 2
1 2
2 3
3 3

Output for Sample Input 2

0

Sample Input 3

10 5
8 3
10 6
5 8
2 7
7 6
1 9
9 3
6 2
4 5
3 5

Output for Sample Input 3

824

---