避けるべし

あなたはいま，上下左右に広大に広がるマス目の原点に当たる位置 (0, 0) にいる．マスの位置はx座標とy座標で表され，右に1マス動くことがx座標が1つ増えることに対応し，上に1マス動くことがy座標が1つ増えることに対応する．あなたはこれから目的地であるマス (x, y) を目指して出発するところだ．あなたは 1 歩で上下左右斜めの 8 方向に隣接するマスに移動することができる．

さあ，目的地に向かって移動開始だ！とあなたは意気込んでいるところかもしれないが，ちょっと待ってほしい．一つだけ先に忠告しておくことがある．それはこのマス目に潜む謎の人物，回り込みのプロ・廻小宮の存在だ．廻小宮はあなたが 1 歩移動したのを確認すると，あなたが進んだ方向のさらに 1 歩先のマスに瞬時に移動し，邪魔をしてくる．より正確に言えば，あなたがマス (x_s, y_s) から (x_t, y_t) に移動するとき，廻小宮は (x_t + (x_t - x_s), y_t + (y_t - y_s)) に移動する．明らかに異様な雰囲気を醸し出す廻小宮．ヤツの間合いに入り込むのは危険だ．回り込まれた直後は仕方ないとして，次に移動する先のマス，あるいはその 8 方向に隣接するマスのどれかに廻小宮がすでにいると，ヤツの間合いに入り込んでしまうことになるので，これはどうしても避けたい．

上記のように廻小宮の間合いを避けつつ，目的地に辿り着くためには最小で何歩必要だろうか？あなたの仕事はこの最小歩数を求めるプログラムを書くことだ．ただし，廻小宮は初期状態ではどのマスにも存在せず，最初の 1 歩目以降から上記のルールに従ったマスに現れるものとする．

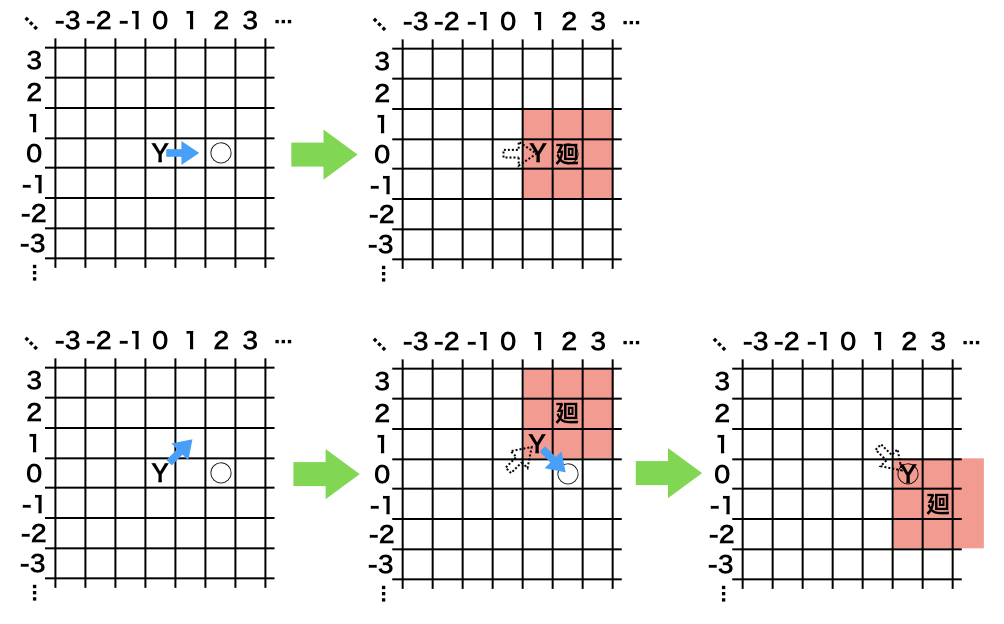
最初のサンプルでは，あなたは (2, 0) を目指す．例えば最初に右横のマス(1, 0) に移動してしまうと，廻小宮が (2, 0) に回り込んでくるため，次にそのマスへと移動することができない．一方，最初に右斜め上の (1, 1) に移動すると，廻小宮の位置は (2, 2) となり (2, 0) が廻小宮の間合いではないため，次の 1 歩で (2, 0) に移動することができる．

Input

入力は複数のデータセットからなる． 各データセットは 2 つの整数 x, y からなる 1 行で表される．これは目的地のマスが位置 (x, y) であることを表し，|x|, |y| ≤ 10⁹ を満たす．

入力の終わりは EOF (ファイルの終端) で表される． 全データセットの総数は 50 を超えない．

Output

条件を満たすように移動を繰り返すとき，マス (0, 0) からマス (x, y) に移動するために必要な最小歩数を 1 行に出力せよ．

Sample Input

2 0
2 2
1 -1
0 0
0 -5
173 207

Output for the Sample Input

2
4
1
0
6
379

---