Problem Statement

Have you experienced $10$-by-$10$ grid calculation? It's a mathematical exercise common in Japan. In this problem, we consider the generalization of the exercise, $N$-by-$M$ grid calculation.

In this exercise, you are given an $N$-by-$M$ grid (i.e. a grid with $N$ rows and $M$ columns) with an additional column and row at the top and the left of the grid, respectively. Each cell of the additional column and row has a positive integer. Let's denote the sequence of integers on the column and row by $a$ and $b$, and the $i$-th integer from the top in the column is $a_i$ and the $j$-th integer from the left in the row is $b_j$, respectively.

Initially, each cell in the grid (other than the additional column and row) is blank. Let $(i, j)$ be the cell at the $i$-th from the top and the $j$-th from the left. The exercise expects you to fill all the cells so that the cell $(i, j)$ has $a_i \times b_j$. You have to start at the top-left cell. You repeat to calculate the multiplication $a_i \times b_j$ for a current cell $(i, j)$, and then move from left to right until you reach the rightmost cell, then move to the leftmost cell of the next row below.

At the end of the exercise, you will write a lot, really a lot of digits on the cells. Your teacher, who gave this exercise to you, looks like bothering to check entire cells on the grid to confirm that you have done this exercise. So the teacher thinks it is OK if you can answer the $d$-th digit (not integer, see an example below), you have written for randomly chosen $x$. Let's see an example.

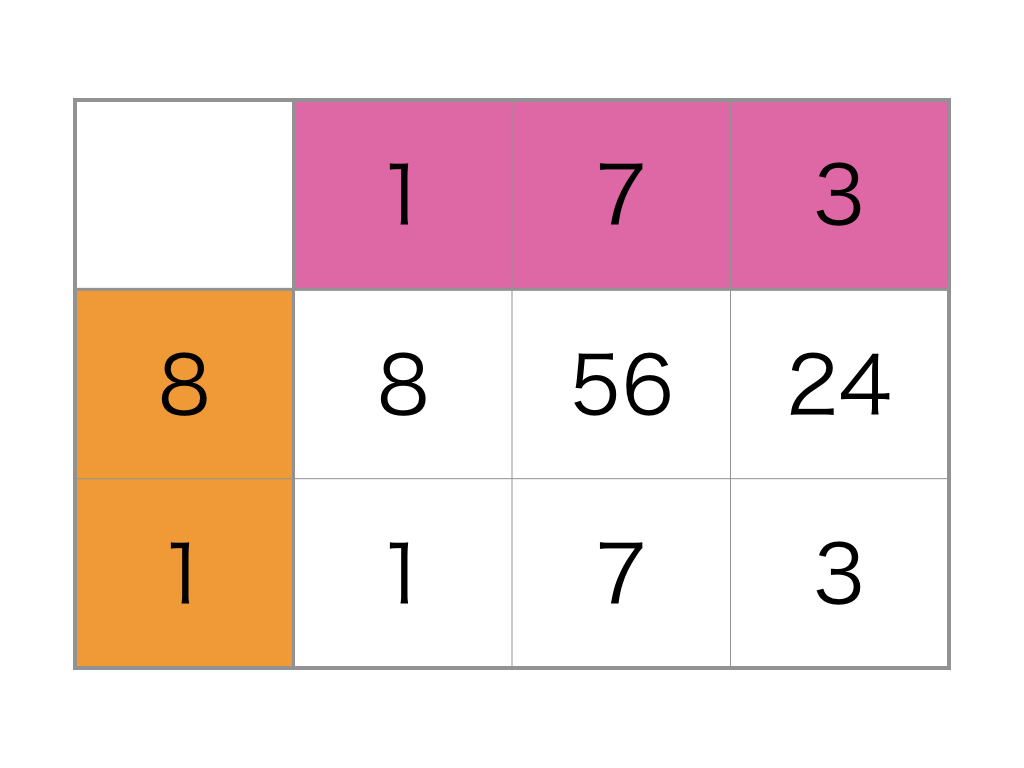
For this example, you calculate values on cells, which are $8$, $56$, $24$, $1$, $7$, $3$ in order. Thus, you would write digits 8, 5, 6, 2, 4, 1, 7, 3. So the answer to a question $4$ is $2$.

You noticed that you can answer such questions even if you haven't completed the given exercise. Given a column $a$, a row $b$, and $Q$ integers $d_1, d_2, \dots, d_Q$, your task is to answer the $d_k$-th digit you would write if you had completed this exercise on the given grid for each $k$. Note that your teacher is not so kind (unfortunately), so may ask you numbers greater than you would write. For such questions, you should answer 'x' instead of a digit.

Input

The input consists of a single test case formatted as follows.

$N$ $M$ $a_1$ $\ldots$ $a_N$ $b_1$ $\ldots$ $b_M$ $Q$ $d_1$ $\ldots$ $d_Q$

The first line contains two integers $N$ ($1 \le N \le 10^5$) and $M$ ($1 \le M \le 10^5$), which are the number of rows and columns of the grid, respectively.

The second line represents a sequence $a$ of $N$ integers, the $i$-th of which is the integer at the $i$-th from the top of the additional column on the left. It holds $1 \le a_i \le 10^9$ for $1 \le i \le N$.

The third line represents a sequence $b$ of $M$ integers, the $j$-th of which is the integer at the $j$-th from the left of the additional row on the top. It holds $1 \le b_j \le 10^9$ for $1 \le j \le M$.

The fourth line contains an integer $Q$ ($1 \le Q \le 3\times 10^5$), which is the number of questions your teacher would ask.

The fifth line contains a sequence $d$ of $Q$ integers, the $k$-th of which is the $k$-th question from the teacher, and it means you should answer the $d_k$-th digit you would write in this exercise. It holds $1 \le d_k \le 10^{15}$ for $1 \le k \le Q$.

Output

Output a string with $Q$ characters, the $k$-th of which is the answer to the $k$-th question in one line, where the answer to $k$-th question is the $d_k$-th digit you would write if $d_k$ is no more than the number of digits you would write, otherwise 'x'.

2 3
8 1
1 7 3
5
1 2 8 9 1000000000000000

853xx

3 4
271 828 18
2845 90 45235 3
7
30 71 8 61 28 90 42

7x406x0