Parse the Syntax Tree
To evaluate a program efficiently, a language processor often transforms it into a syntax tree. In this problem you are given a syntax tree of a mathematical expression using ASCII characters. Please evaluate the expression.
The syntax tree we consider in this problem is a rooted binary tree where each node has either zero or two children. If a node has zero children, it is an integer node that corresponds to a single integer between 0 and 9, inclusive. On the other hand, if a node has two children, the node is a binary operation node that corresponds to a binary operation of either addition, subtraction or multiplication. In this case the left and right children correspond to the left and right operands of the binary operation, respectively. For example, Figure B.1 represents the syntax tree of expression (9 - 4) * ((7 * 2) + 5).
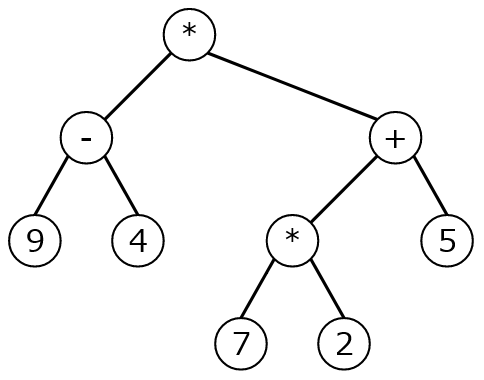
To represent such a syntax tree using ASCII characters, you are given $H$ strings of $W$ characters. Each character is either '+', '-', '*', a digit between '0' and '9', or a period that represents a blank. For example, here is the representation of the syntax tree of Figure B.1.
...*..... .-.....+. 9.4..*..5 ....7.2..
Figure B.2 shows the rules (similar to Backus-Naur Form) of such representation of a syntax tree.
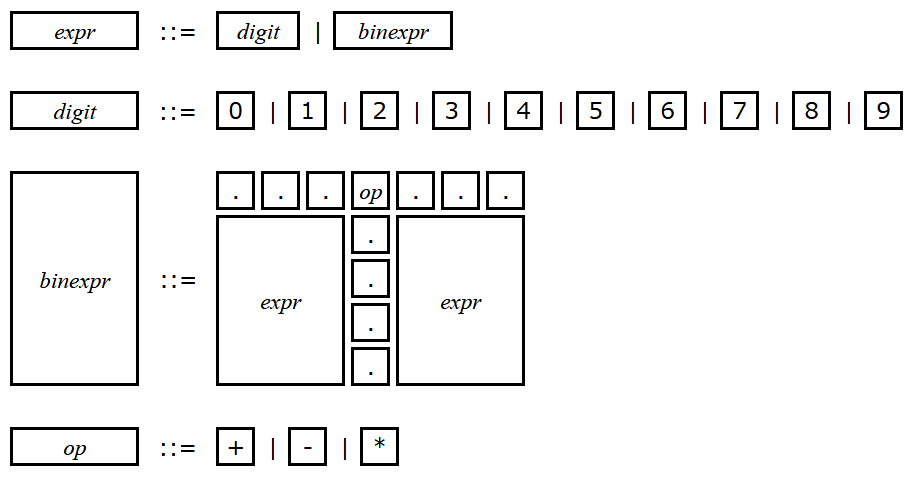
More precisely, the rules are defined as follows.
- A "cell" is a rectangular region of characters that corresponds to a single node (i.e., either an integer node or a binary operation node) of a syntax tree.
- A cell corresponding to an integer node contains only a single digit that is the same integer of the node. The height and width of such a cell are 1.
- A cell $c$ corresponding to a binary operation node $v$ contains a single operator and two other cells as children. More precisely, let $v_1$ and $v_2$ be the left and right children of the binary operation node, respectively. And let $c_1$ and $c_2$ be the cells that correspond to $v_1$ and $v_2$, respectively. The height of $c$ is $max(h_1, h_2)+1$ where $h_1$ and $h_2$ are the heights of $c_1$ and $c_2$, respectively. On the other hand, the width of $c$ is $w_1+w_2+1$ where $w_1 $and $w_2$ are the widths of $c_1$ and $c_2$, respectively. The topmost row of $c$ consists of $w_1$ periods followed by an operator followed by $w_2$ periods where the operator is either '+', '-' or '*'. $c_1$ is located from the second to the $(h_1+1)$-st rows (from the top) and the first to the $w_1$-st columns (from the left) of $c$. Similarly, $c_2$ is located from the second to the $(h_2+1)$-st rows (from the top) and the $(w_1+2)$-nd to the $(w_1+w_2+1)$-st columns (from the left) of $c$. Note that although $c_1$ and $c_2$ may have different heights, their top borders are always aligned.
- It is guaranteed by the above rules that no two cells partially overlap each other. In other words, when two cells overlap, then one of them completely contains the other.
- Any other characters that are not restricted by the above rules are filled by periods.
- The entire region of characters is the "root" cell. In other words, the cell corresponding to the root node of the syntax tree has height $H$ and width $W$.
Your task is to calculate the mathematical expression that corresponds to the given syntax tree formatted by the above rules.
Input
The input consists of a single test case of the following format.
$H$ $W$ $s_1$ : $s_H$
The first line contains two integers $H$ and $W$ ($1 \leq H, W \leq 37$), which represent the height and width of the representation of the given syntax tree. The following $H$ lines consist of strings of length $W$ where each character is either '+', '-', '*', a digit between '0' and '9', or a period. It is guaranteed that these strings represent a syntax tree of a mathematical expression in a valid form.
Output
Print the calculation result of the mathematical expression that corresponds to the given input.
Sample Input 1
1 1 5
Sample Output 1
5
Sample Input 2
2 3 .-. 9.2
Sample Output 2
7
Sample Input 3
4 9 ...*..... .-.....+. 9.4..*..5 ....7.2..
Sample Output 3
95