Problem Statement
整数 $N$ と整数 $X_i, H_i, R_i\ (1 \leq i \leq N)$ が与えられます。 実数上の関数 $f$ を以下のように定義します。
$$f(x)= \sum_{i=1}^{N} \max \left( 0, H_i \left(1 - \frac{2|x - X_i|}{R_i}\right) \right)$$
実数上で関数 $f$ がとる最大値 $\displaystyle \max_{x\in\mathbb{R}} f(x)$ を求めてください。
Constraints
- $1 \leq N \leq 100{,}000$
- $1 \leq X_i \leq 10^{8}$
- $1 \leq H_i \leq 10^{8}$
- $1 \leq R_i \leq 10^{8}$
- 全ての入力は整数である
Input
1行目に $N$ が与えられる。 続く $N$ 行は $X_i,H_i,R_i$ が空白区切りで与えられる。
$N$ $X_1$ $H_1$ $R_1$ $\vdots$ $X_N$ $H_N$ $R_N$
Output
$f(x)$ の最大値を1行目に出力してください。 なお、想定解から$10^{-6}$までの相対誤差は正答扱いとします。
Sample
Sample Input 1
2 10 2 2 10 4 4
Sample Output 1
6.0000000000
この入力例では $f(x)$ の値は次のようになります。
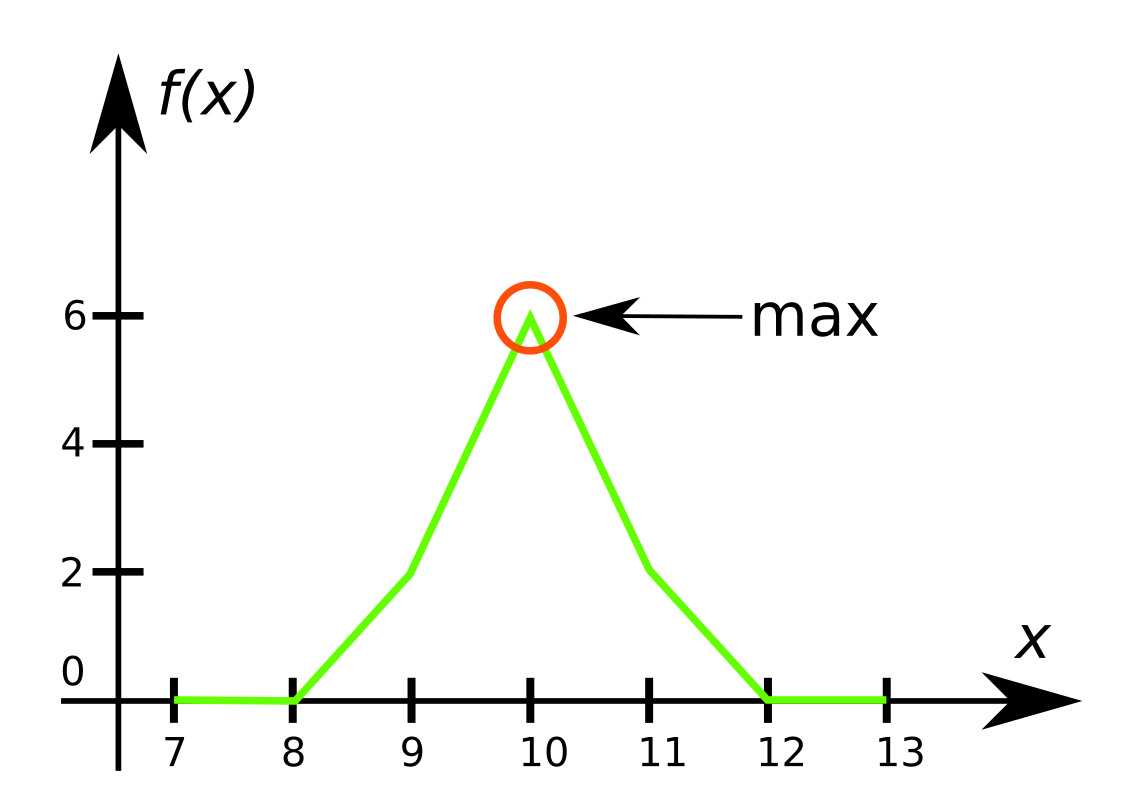
また、この入力に対する解答として $6$ や $6.0$ なども有効です。
Sample Input 2
3 1 10 10 5 4 6 7 2 6
Sample Output 2
10.0000000000
Sample Input 3
6 1 3 10 2 3 10 3 3 10 4 3 10 5 3 10 6 3 10
Sample Output 3
12.6000000000