積分

$y = x^2$
$y = 0$
$x = 600$

という３つの線で囲まれる部分の面積を求める方法について考えます。高校で学習する積分を利用するとその面積は $72000000$ であるとわかりますが、下図のような多数の長方形の面積の和を求めることによって、それに極めて近い値を得ることができます。

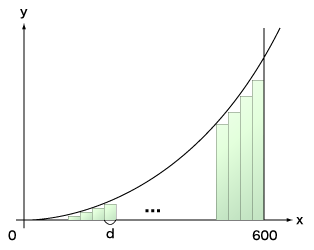
$f(x) = x^2$

長方形の横の長さを $d$ とおくと、面積 $s$ の近似的な値は

縦の長さが $f( d )$ で横の長さが $d$ である長方形の面積 $+$
縦の長さが $f( 2d )$ で横の長さが $d$ である長方形の面積 $+$
縦の長さが $f( 3d )$ で横の長さが $d$ である長方形の面積 $+$
...
縦の長さが $f( 600 - d )$ で横の長さが $d$ である長方形の面積

となります。$d$ を小さくすればするほど、この値は $72000000$ に近づきます。

$600$ の約数 $d$ を入力として受け取り、上記の方式で求めた近似的な面積を出力するプログラムを作成して下さい。

Input

複数のデータセットが与えられます。各データセットには整数 $d$ が１行に与えられます。入力の最後まで処理して下さい。

データセットの数は 20 を超えません。

Output

各データセットに対して、近似的な面積 （整数）を１行に出力して下さい。

Sample Input

20
10

Output for the Sample Input

68440000
70210000

---