カード

正の整数が書かれた一組のカードがあります。カードを積んで山をいくつか作り、それらを横一列に並べます。その中から隣り合った 2 つのカードの山を選び、右側の山の上に左側の山をそのまま重ねます。この操作をカードの山が一つになるまで繰り返していきます。

2 つのカードの山を重ねる時にそれらの一番上と下のカードに書かれた数をすべて掛け合わせます。こうして得られた数をカードの重ね合わせのコストと呼ぶことにします。カードの山を一つにするためのコストはすべての重ね合わせのコストを足し合わせたものとします。

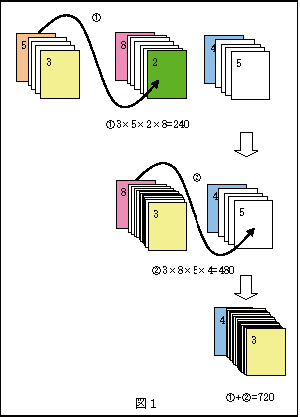
どのような順番でカードの山を重ねるかでコストは変わります。たとえば、3 つのカードの山がある場合を考えます。それらの一番上と下のカードに書かれた数が，左側の山から順にそれぞれ 3 と 5, 2 と 8, 5 と4 だったとします。このとき，はじめに左と真ん中の山を重ねたときのコストは、3 × 5 × 2 × 8 = 240 です。この重ね合わせによって、一番上のカードが 3 で一番下のカードが 8 である山ができます。

この山を右の山の上に重ねると、そのコストは 3 × 8 × 5 × 4 = 480 になります。したがって、この順番でカードの山を一つにまとめたときのコストは 240 + 480 = 720 です。（図1）

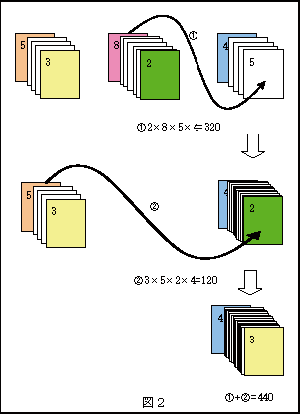
一方、はじめに真ん中と右の山を重ねてから最後に左の山を重ねることにすると、そのときのコストは 2 × 8 × 5 × 4 + 3 × 5 × 2 × 4 = 440 になります。したがって，後の場合のように重ねた方がコストが小さくなります。（図2）

カードの山の個数とそれぞれの山の一番上と下のカードに書かれた数を入力とし、カードの山を一つにまとめるのに必要な最小のコストを出力するプログラムを作成してください。ただし、山の個数は 100 個以下とし、入力されるデータはどのような順番でコストを計算しても 2³¹-1 を超えることはありません。

Input

入力は以下の形式で与えられます。

n
a1 b1
a2 b2
:
an bn

1 行目にカードの山の個数 n(n ≤ 100)、続く n 行に左から i 番目の山の 1 番上のカードに書かれた数 a_i (1 ≤ a_i ≤ 200) と 1 番下のカードに書かれた数 b_i (1 ≤ b_i ≤ 200) が与えられます。

Output

カードの山を一つにまとめるのに必要な最小のコストを１行に出力してください。

Sample Input

3
3 5
2 8
5 4

Output for the Sample Input

440

---