ふしぎな虫
会津生物学研究所のA博士は、とある南の島でふしぎな虫を発見しました。形は芋虫のように細長いのですが、ひとつの体節が玉のような形をしているので、糸でつないだビーズ玉のように見えます。ふしぎなのは体の色に様々なバリエーションがあることと、なかには時間がたつにつれて体の色が変っていく虫がいることでした。どの虫の体節の色も赤か緑か青のどれかに限られるようですが、1 秒ごとに体節の色が変わっていき、最後にはすべての体節が同じ色になって落ち着く場合もあれば、いつまで待ってもずっと色が変わりつづける場合もあるようでした。

調べていくうちに、ふだんはすべての体節が同じ色をしているのですが、何かに驚いたりして興奮した後は体節の色が勝手に変わってしまうことがわかりました。一度体節の色が変わってしまうと、ふたたびすべての体節が同じ色になるまではずっと色が変わり続けることがわかりました。
A博士はこの虫を何匹も捕まえて興奮させてみては、色が変わる様子を興味深く観察していましたが、やがて色が変化している最中の色の変わり方には次のような規則性があることに気がつきました。
- 色が変わるのは、隣り合っている色違いの 2つの体節のペア 1組だけが変わり、他の体節の色は変わらない。ただし、そのようなペアが複数あるときに、どのペアの色が変わるかはあらかじめ予測できない。
- そのようなペアは、2つの体節の色のどちらでもない色に同時に変わる(たとえば、緑と赤の体節が隣り合っているときは、それらが同時に青に変わる)。
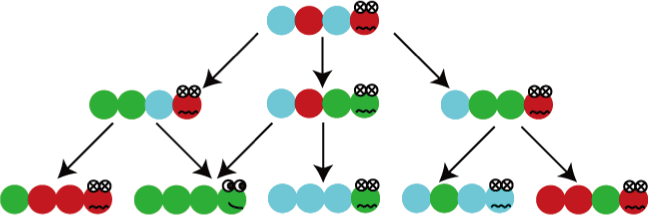
虫の色の変化を、2秒後まですべて書いたものが上の図です。図の上段のような色をした虫がいるとします。このとき、隣り合った色違いの体節のペアは 3組あるので、1秒後には中段に並べて描いた 3通りの色のどれかに変わります。1秒後に中段左側の 2つのように変わったときには、2秒後にすべての体節が緑色になることができます(図の下段の左側から 2番目)。 それに対して、1秒後に中段の1番右のように変わったときには、2秒後にすべての体節が同じ色に変わることはありません。
博士は、目の前にいる虫の体節がすべて同じ色になる可能性があるのか、あるとしたらそうなるのは最短で何秒後なのかを予測することにしました。
目の前にいる虫の体節の色の並びを入力とし、その虫の体節がすべて同じ色になるのに要する最短の時間を秒単位で出力するプログラムを作成してください。ただし、同じ色になる可能性がないときは「NA(半角英大文字)」と出力してください。また、虫の体節の色の並びは2 以上 10 以下のr(赤)、g(緑)、b(青)からなる文字列で表されます。
Input
複数のデータセットの並びが入力として与えられます。入力の終わりはゼロひとつの行で示されま す。各データセットとして、 虫の体節の情報を表す1つの文字列が1行に与えられます。
データセットの数は 100 を超えません。
Output
データセット毎に、すべての体節の色が同じになるまでに要する最小時間 (秒単位の整数) または NA を1行に出力します。
Sample Input
rbgrg rbbgbbr bgr bgrbrgbr bggrgbgrr gbrggrbggr rrrrr bgbr 0
Output for the Sample Input
5 7 1 6 NA 8 0 4