会津の埋蔵金

会津には古くから伝わる埋蔵金の伝説があります。あなたは、遂に埋蔵金が埋まっている場所を突き止めました。埋蔵金が埋まっている深さ、掘り進める地層の状態が分かっているので、綿密に計画を立てれば最小費用で埋蔵金まで到達することができます。そこであなたは、地層の状態を読み取って埋蔵金の埋まっている深さまで最小費用で到達するルートを算出するプログラムを作成することにしました。

地層の状態は 2 次元格子状に配置されたセルで表わされ、各セルの位置は座標 (x,y) で表されます。左上を (1,1) とし、x 座標は右に行くにつれて大きくなり、y 座標は下に深くなるにつれて大きくなるものとします。あなたは y 座標の一番小さいセルのうち一つを選んでそこから掘り始め、y 座標の一番大きいセルの一つまで掘り進めます。地層には以下の 2 種類のセルがあります：

1. 土の詰まったセル。掘るのに、セルごとに決められた費用がかかる。
2. 酸素のたまったセル。掘る必要はなく、セルごとに決まった量の酸素を補給できる。一度酸素を補給したセルの酸素はなくなり、再度の補給はできない。また、このセルに辿りついたら必ず酸素の補給をしなければならない。

あるセルから掘ることができるのは左右と下方向のセルのみです。 一度掘ったセルを左右に移動することはできますが、上に移動することはできません。

発掘にあたっては、酸素ボンベを携帯しなければなりません。酸素ボンベの残量が 0 になった瞬間、移動も発掘も酸素の補給もできなくなります。残量はセルを移動するたびに 1 減ります。酸素ボンベの残量が 0 で埋蔵金の埋まっている深さまで到達しても、到達したとみなされません。また、酸素のたまったセルでは酸素を補給することができますが、容量を超えた分は廃棄されます。

地層のサイズ 、発掘費用、酸素ボンベの容量、初期状態で持っている酸素の量、地層の情報を入力とし、一番深いセルまでたどりつくための最小費用を出力するプログラムを作成してください。ただし、最小費用が発掘費用を超えてしまう場合や、どのように掘り進めても埋蔵金にたどりつけない場合は“NA”と出力してください。

Input

複数のデータセットの並びが入力として与えられる。入力の終わりはゼロふたつの行で示される。 各データセットは以下の形式で与えられる。

W H
f m o
c1,1 c2,1 ... cW,1
c1,2 c2,2 ... cW,2
...
c1,H c2,H ... cW,H

１行目に地層の横方向のサイズ W, 縦方向のサイズ H (3 ≤ W, H ≤ 10) が与えられる。 ２行目にあなたの発掘費用を表す整数 f (1 ≤ f ≤ 10000)、酸素ボンベの容量を表す整数 m (3 ≤ m ≤ 50)、初期状態で持っている酸素の量を表す整数 o (o ≤ m) が与えられる。

続く H 行に地層の情報 c_i,j が与えられる。c_i,j は、座標 (i, j) に対するセルの情報を表し、以下の形式で与えられる：
負の値の場合、土の詰まったセルで、値は費用を表す
正の値の場合、酸素のたまったセルで、値は酸素の量を表す
ただし、酸素のたまったセルは 50 箇所以内である。

データセットの数は50 を超えない。

Output

データセットごとに、最少費用または NA を1行に出力する。

Sample Input

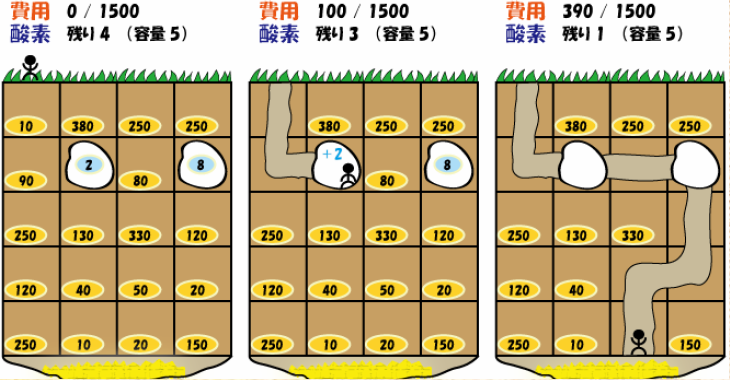
3 3
100 10 10
-100 -20 -100
-100 -20 -100
-100 -20 -100
3 3
100 10 10
-100 -20 -100
-100 -20 -20
-100 -60 -20
3 3
100 10 3
-100 -20 -100
-20 -20 -20
-20 -100 -20
3 3
100 3 3
-100 -20 -30
-100 -20 2
-100 -20 -20
4 5
1500 5 4
-10 -380 -250 -250
-90 2 -80 8
-250 -130 -330 -120
-120 -40 -50 -20
-250 -10 -20 -150
0 0

Output for the Sample Input

60
80
NA
50
390

---