Salary for a Plumber
I am a pipe joiner. As long as I have a pipe joint and a pipe to connect, I can connect any pipe. Every day, I am given pipes and joints by my master, and I connect them and hand them to him. But if there are too many pipes, I can't connect them all in one day. Even in such cases, the master smiles and hands me my salary.
By the way, one day I noticed something strange. I often got paid more when I couldn't connect all the pipes than when I could connect them. It was so strange that one day, when the master came to see me, I sneaked a look at the memo on how the salary was calculated. Then I found out that
" Salary is to be paid in 'the number of pipes x the sum of the lengths of the pipes. However, if the pipes are connected by joints to form a single connection, it shall be considered as one pipe."
Now we know why it is sometimes cheaper to connect all of them together to get a lower salary. For example, as shown in the figure below, if we connect all three pipes of length 1 and two joints of length 2, we get one pipe of length 1+2+1+2+1 = 7, so 1 × (7) = 7. But if we use only one joint to make two pipes, one with length 1+2+1 = 4 and the other with length 1, we get 2 × (4+1) = 10, so we get paid more than if we connect them all.
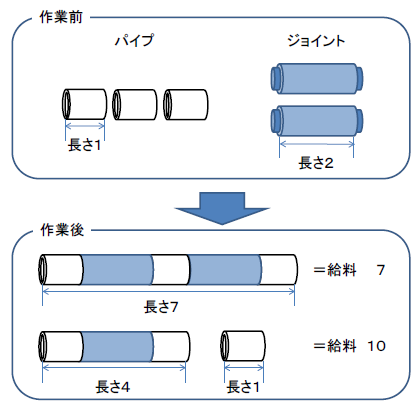
I don't know why the master uses this method to determine the salary, but now I know how I can get paid more too!
Given the number of pipes, create a program to calculate the maximum amount of salary you can get.
Input
The input consists of multiple data sets. The end of the input is indicated by a line with zero one. Each data set is given in the following format.
n p1 ... pn j1 ... jn-1
The first line gives the number of pipes, n (2 ≤ n ≤ 65000). The second line consists of n integers separated by a space. pi (1 ≤ pi ≤ 1000) indicates the length of the i-th pipe. The third line consists of n-1 integers separated by a single space. ji (1 ≤ ji ≤ 1000) indicates the length of the i-th joint.
The i-th joint can only connect the i-th and i+1-th pipes. The length of the connected pipes will be pi + ji + pi+1.
The number of data sets does not exceed 100.
Output
For each data set, output the maximum amount of salary that can be obtained on a single line. For the data sets given as input, the output value should always fall in the range of 32-bit unsigned integers.
Sample Input 1
3 1 1 1 3 3 4 3 3 3 3 1 1 1 5 1 2 3 4 5 4 3 2 1 0
Sample Output
12 48 76