パイプつなぎ職人の給料
ぼくはパイプつなぎ職人です。パイプをつなぐジョイントとパイプさえもらえれば、どんなパイプだってつないでみせます。ぼくは毎日、親方からパイプとジョイントを渡されて、それをつないで親方に渡します。でも、パイプの数が多すぎるときは、1日でそれを全部つなげることはできません。そんなときでも親方はにっこり笑って、ぼくに給料を渡してくれます。
ところで、あるとき変なことに気がつきました。全部のパイプをつなげられたときより、つなげられなかったときの方が給料が多いことがしょっちゅうあるんです。あんまり変なので、ある日、親方が来たときに、給料の計算方法が書いてあるメモをこっそり見ちゃいました。そしたら、なんと
"給料は「パイプの本数×パイプの長さの総和」で支払う。ただし、ジョイントでつなげて、ひとつながりになったものは、それを1本のパイプとみなす。"
って書いてありました。これで全部つなげた方が給料が安くなることがある理由がわかりました。たとえば下図のように、長さ 1 のパイプ 3 本と長さ 2 のジョイント 2 本を全部つなげると長さ 1+2+1+2+1 = 7 のパイプが 1 本できるので、1 × (7) = 7 です。でも、ジョイントを一つだけ使って長さ 1+2+1 = 4のパイプと長さ 1 のパイプの 2 本にすると2 × (4+1) = 10なので、全部つなげるよりいっぱい給料がもらえます。
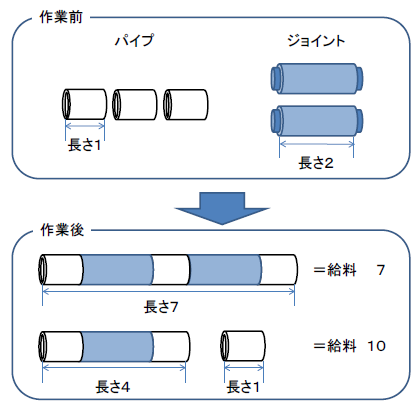
親方がなんでこんな方法で給料を決めてるかわからないけど、これでぼくもどうすればもらえる給料を多くできるかわかりました!
それでは、パイプの本数が与えられたとき、もらえる給料の最大の金額を計算するプログラムを作成してください。
入力
入力は複数のデータセットからなる。入力の終わりはゼロ1つの行で示される。各データセットは以下の形式で与えられる。
n p1 ... pn j1 ... jn-1
1行目にパイプの本数 n (2 ≤ n ≤ 65000) が与えられる。2行目は1つの空白で区切られた n 個の整数からなる。pi (1 ≤ pi ≤ 1000) はi番目のパイプの長さを示す。3行目は1つの空白で区切られた n-1 個の整数からなる。ji (1 ≤ ji ≤ 1000) は i 番目のジョイントの長さを示す。
i番目のジョイントは、i 番目と i+1 番目のパイプだけをつなげることができる。つなげたパイプの長さは、pi + ji + pi+1 になる。
データセットの数は 100 を超えない。
出力
各データセットごとに、得られる給料の最大の金額を1行に出力する。入力として与えられるデータセットでは、出力される値は必ず32ビット符号無し整数の範囲に収まるものとする。
入力例1
3 1 1 1 3 3 4 3 3 3 3 1 1 1 5 1 2 3 4 5 4 3 2 1 0
出力例
12 48 76