Ruins

The Aizu Archaeological Society has set out to investigate the ruin of the ancient nation of Iwashiro, which is submerged in the Hibarra Sea. The ruin exists somewhere in the Hibara Sea. We decided to use radar to get a rough idea of the location of the ruin from the shoreline, and to estimate how many meters away from the shoreline we would have to go to investigate.

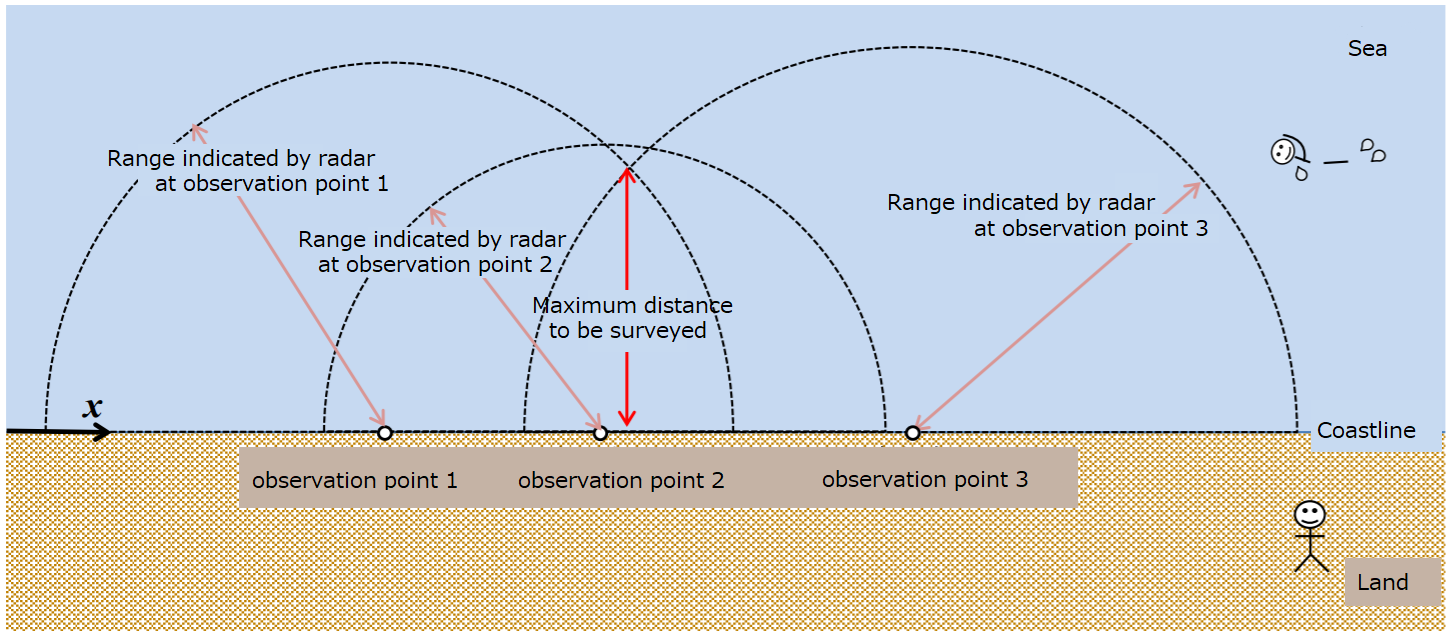
The observation points are placed on the coastline represented by the straight line as shown in the figure above, and the exploration radars are placed there. The radar can only tell us that there is the ruin within a semicircle of a certain size centered on the observation point. However, by combining multiple observation data, it is possible to narrow down the area to a smaller one.

Given some observation data, consisting of the location of the observation points and the radius indicated by the exploration radars, write a program to find out how far from the coastline we need to survey at most.

Input

The input is given in the following format.

N
x1 r1
x2 r2
:
xN rN

The first line gives the number of data measured by the exploration radar N (1 ≤ N ≤ 100000). The following N lines are integers x _i that represents the position of the observed data i on the coastline in meters (0 ≤ x _i ≤ 1,000,000) and integers r _i that represents the number of meters within a radius of the site (1 ≤ r _i ≤ 1,000,000). Two or more observation data with the same observation point may be given.

If there are multiple observational data given, it can be considered that there is always a point included in all of those semicircles.

Output

Outputs the actual number of meters that need to be investigated from the coastline. However, the error must not exceed plus or minus 0.001 meters. If this condition is satisfied, any number of digits after the decimal point may be displayed.

Sample Input 1

2
0 2
1 2

Sample Output 1

1.936

Sample Input 2

3
0 3
1 2
2 1

Sample Output 2

1.0

Sample Input 3

2
0 1
3 2

Sample Output 3

0.0

---