Stopwatch Without a Scale

　

There is a stopwatch like the one shown in the figure. This stopwatch has no scale, except for a single marker indicating zero. The moment it is started, the hand points to the marker, and from there the hand rotates clockwise at a constant rate around the axis. Since there is no scale, it is not possible to directly read the time elapsed since start-up. Instead, we know that the elapsed time is $t$ seconds when the hand turns $a$ degree clockwise from the marker. Note that $a$ must be less than 360 degrees.

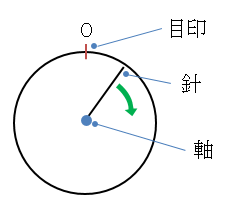
Given the angle $a$ and the elapsed time $t$, write a program to find the elapsed time represented by the angle $r$ of the hand read after the stopwatch is started. It is assumed that it is known that the hand has not gone around.

Input

The input is given in the following form.

$a$ $t$ $r$

Angle $a$ ($1 \leq a \leq 359$) and elapsed time $t$ at angle $a$ ($1 \leq t \leq 1,000$), and read angle $r$ ($0 \leq r \leq 359$) are all given as integers. The units of $a$ and $r$ are degrees, and the unit of $t$ is seconds.

Output

Output the elapsed time represented by the angle of the hand read in seconds as a real number in a line. The error must not exceed plus or minus 0.001.

Sample Input and Output

Sample Input 1

180 120 90

Sample Output 1

60.0

Sample Input 2

90 100 120	

Sample Output 2

133.333333

---