Processing Machine

Aizu Kogyo undertakes manufacturing work using a processing machine. The processing machine owned by Aizu Kogyo is shown on the left in Figure 1. This machine can process any rectangular object, and its width, depth, and height can be freely set. There is a blade 1 cm wide and 1 cm deep on the top of this rectangular object. This blade can be moved directly above the position where you want to cut. The position where you want to cut is specified by the coordinates of the compartment as shown in the right side of Figure 1.

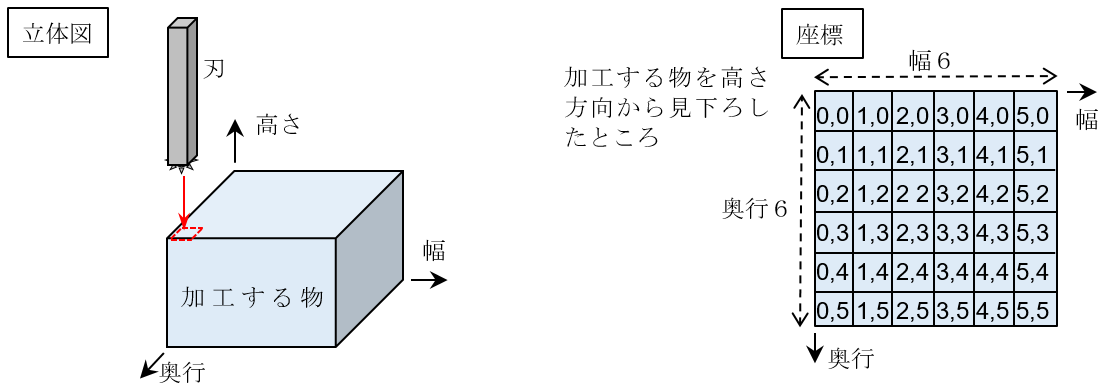
Figure 1: 3D view of the machine and the coordinates of the compartment

The machine will cut a rectangular object by repeating the following steps.

• Move the blade to directly above the specified section.
• Lower the blade until it touches the object to be machined, and then cut a new section of the specified length.
• Raise the blade and bring it back to the initial height.

An example of shaving one of the end sections is shown in Figure 2.

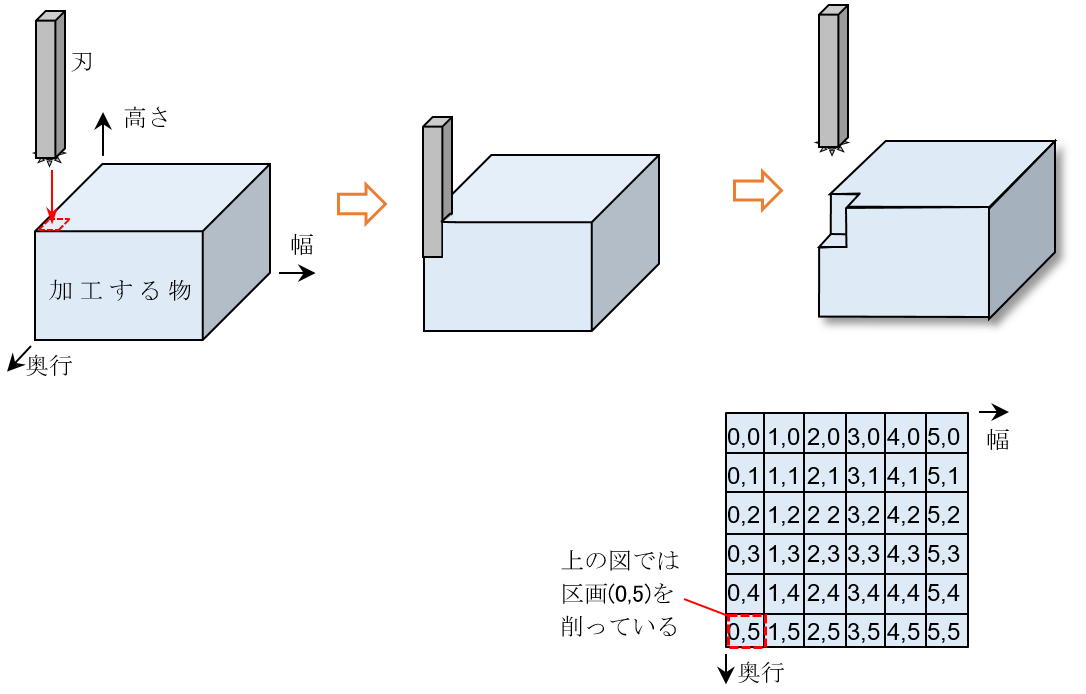
Figure 2: Example of cutting using a processing machine

At Aizu Industries, we determine the processing fee based on the amount of surface area after processing. Until now, this has been measured manually by craftsmen, but we would like to be able to calculate this using a program.

Given the size of the rectangular object to be machined and information on how the rectangular object is to be machined, write a program that calculates how much the surface area will be after machining.

Input

The input is given in the following form.

$W$ $D$ $H$ $C$
$x_1$ $y_1$ $z_1$
$x_2$ $y_2$ $z_2$
:
$x_C$ $y_C$ $z_C$

In the first line, the width $W$ ($1 \leq W \leq 100,000$), depth $D$ ($1 \leq D \leq 100,000$), height $H$ ($1 \leq H \leq 100,000$), and the number of cuts $C$ ($0 \leq C \leq 100,000$) of the rectangle to be machined are given. In the following $C$ lines, the information on how to cut the rectangle is given. $x_i$ ($0 \leq x_i < W$) and $y_i$ ($0 \leq y_i < D$) are the coordinates of the plot to be cut. Also, $z_i$ ($1 \leq z_i < H$) is an integer that represents how much the plot should be cut from its current height. However, for each parcel, no input is given such that the height after shaving will be less than 1.

Output

Output the surface area after processing a line.

Sample Input and Output

Sample Input 1

3 4 5 2
0 0 4
1 1 4

Sample Output 1

110

Sample Input 2

1 2 3 0

Sample Output 2

22

Since Sample Input 2 is a case where the surface area is never scraped, the surface area is the same as the surface area of ​​the given rectangular.  

---