Placement Games

PCK bought a new game to accompany his long autumn nights. The game board is rectangular in shape, divided into equal-sized square sections of $H$ in vertical direction and $W$ in horizontal direction. The player places one rectangular piece on the board that uses $R$ of vertical space and $C$ of horizontal space, aligning it with the boundaries of the sections. However, there are some obstacles placed in the sections, and you cannot place a piece in such a way that it uses a section with an obstacle. Also, the pieces must not be placed in different directions.

The number of points in this game is determined by the number of sections in the same row or column as the section of pieces placed, which meet the following conditions:

It is not a section where pieces or obstacles are placed.

When you move straight from each section to a piece, either vertically or horizontally, you can reach the piece without encountering any obstacles.

For example, suppose we have a board with $H=4$ and $W=5$ as shown in (a) below. The $(r,c)$ on the board represents the number of the sections, and there are obstacles in sections $(2,3)$, $(3,5)$, and $(4,4)$. As shown in (b) below, suppose a player places a piece of size $R=1$, $C=2$ using the sections $(3,2)$ and $(3,3)$. In this case, there are 9 sections $(1,2),(1,3),(2,2),(2,3),(3,1),(3,4),(3,5),(4,2),(4,3)$ in the same row and column as the placed piece, excluding the section where the piece was placed. Of these, the sections marked with a "+" in (c) below satisfy the above condition. The number of such sections is the score in this game, and in this case the score is 6.

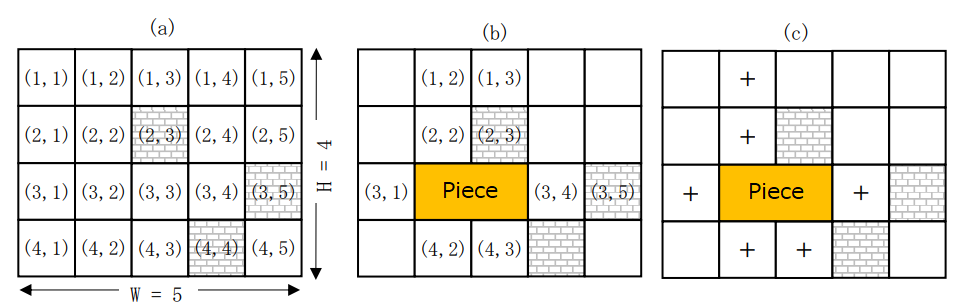
PCK is trying to figure out the maximum number of points he can score with various board and piece sizes.

Given the information on the game board and the size of the pieces to be placed, write a program to find the maximum number of points that can be scored in the game.

Input

The input is given in the following format.

$H$ $W$ $R$ $C$
$N$
$r_1$ $c_1$
$r_2$ $c_2$
:
$r_N$ $c_N$

In the first line, we are given the number of vertical sections of the board $H$ ($1 \leq H \leq 1000$), the number of horizontal sections $W$ ($1 \leq W \leq 1000$), the number of vertical sections occupied by pieces $R$ ($1 \leq R \leq H$), and the number of horizontal sections $C$ ($1 \leq C \leq W$) are given. In the next line, the number of obstacles $N$ ($0 \leq N \leq 10,000$) is given. However, $N$ will not exceed $H \times W - R \times C$. In the subsequent $N$ line, the location of the obstacle is given. $r_i$ ($1 \leq r_i \leq H$) and $c_i$ ($1 \leq c_i \leq W$) are integers representing the vertical and horizontal positions, respectively. However, the position of the section in the upper left corner is set to $r=1,c=1$. The same position is never given more than once. You can assume that there is always at least one way to place a piece.

Output

Output the maximum number of points that PCK can obtain on one line.

Sample Input and Output

Sample Input 1

4 5 1 2
3
2 3
3 5
4 4

Sample Output 1

9

Sample Input 2

5 4 4 3
0

Sample Output 2

7

---