配置ゲーム
PCK君は秋の夜長のお供に新しいゲームを買いました。ゲームの盤面は全体が長方形で、縦に$H$個、横に$W$個の、同じ大きさの正方形の区画に分かれています。プレイヤーは、縦に$R$個、横に$C$個分の区画を使う長方形の駒を一つ、区画の境界に合わせるようにして盤面に配置します。しかし、区画にはいくつかの障害物が配置されていて、障害物がある区画を使うような駒の置き方はできません。また、駒の向きを変えて配置してはいけません。
このゲームの点数は、配置した駒の区画と同じ行または同じ列にある区画のうち、以下の条件を満たす区画の数で決まります。
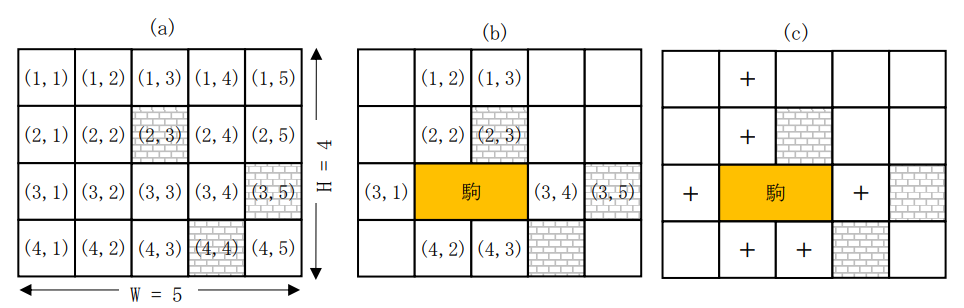
たとえば、下図(a)のような$H=4$, $W=5$の盤面があるとします。盤面の$(r,c)$は区画の番号を表しており、区画$(2,3)$と$(3,5)$と$(4,4)$に障害物があります。下図(b)のように、プレイヤーが大きさ$R=1$, $C=2$の駒を、区画$(3,2)$と$(3,3)$を使って置くとします。このとき、置いた駒と同じ行、同じ列にある区画で、駒が置かれた区画を除いたものは$(1,2),(1,3),(2,2),(2,3),(3,1),(3,4),(3,5),(4,2),(4,3)$の9個あります。これらのうち、下図(c)の「+」を付けた区画が、上の条件を満たします。そのような区画の数がこのゲームでの点数となり、この場合の点数は6点です。
PCK君は、いろいろな盤面や駒のサイズで、最大何点取れるかを考えています。
ゲームの盤面の情報と配置する駒のサイズが与えられたとき、ゲームで最大何点取れるかを求めるプログラムを作成せよ。
入力
入力は以下の形式で与えられる。
$H$ $W$ $R$ $C$ $N$ $r_1$ $c_1$ $r_2$ $c_2$ : $r_N$ $c_N$
1行目に盤面の縦方向の区画の数$H$ ($1 \leq H \leq 1000$)と横方向の区画の数$W$ ($1 \leq W \leq 1000$)、駒が縦方向に占める区画の数$R$ ($1 \leq R \leq H$)と横方向に占める区画の数$C$ ($1 \leq C \leq W$)が与えられる。続く1行に障害物の数$N$ ($0 \leq N \leq 10,000$)が与えられる。ただし、$N$は$H \times W - R \times C$を超えない。続く$N$行に、障害物の位置が与えられる。$r_i$ ($1 \leq r_i \leq H$)と$c_i$ ($1 \leq c_i \leq W$)はそれぞれ縦方向と横方向の位置を表す整数である。ただし、左上隅の区画の位置を$r=1,c=1$とする。同じ位置が2回以上与えられることはない。駒を置く方法は必ず一通り以上はあると考えてよい。
出力
PCK君が獲得できる得点の最大値を1行に出力する。
入出力例
入力例1
4 5 1 2 3 2 3 3 5 4 4
出力例1
9
入力例2
5 4 4 3 0
出力例2
7