Star-shaped Pentagon

A witch lived deep in the woods in the middle of nowhere. Her magic is triggered by drawing a magic circle on the ground. This magic circle is activated when five stones A, B, C, D, and E are placed on the ground, and when these stones are connected in the order of A→ B→ C→ D→ E→ A, they form a star-shaped pentagon.

Given five different points A, B, C, D, and E in the two-dimensional plane, in that order. However, no three points can be on the same line. Create a program to determine whether a star-shaped pentagon can be drawn by lines AB, BC, CD, DE, and EA.

In a convex pentagon where the sum of the interior angles of the adjacent vertices is greater than 180 degrees, if each side is extended to one side and the points of intersection are connected by straight lines, a star-shaped pentagon is drawn. Figure (a) shows an example of how a star-shaped pentagon is created from a convex pentagon in this way. As shown in Figure (b), the star-shaped pentagon can be drawn by connecting points A, B, C, D, and E in the order A→B→C→D→E→A.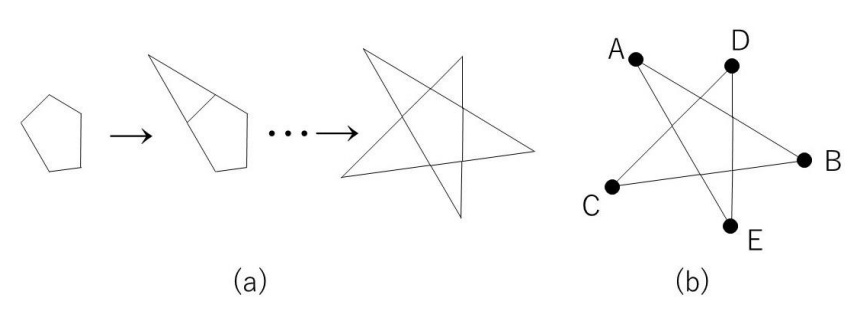

Input

The input is given in the following format.

$x_1$ $y_1$
$x_2$ $y_2$
$x_3$ $y_3$
$x_4$ $y_4$
$x_5$ $y_5$

The coordinates $x_i$ and $y_i$ ($0 \leq x_i \leq 100$, $0 \leq y_i \leq 100$) of the five points A, B, C, D, and E are given in turn, each on one line. However, the coordinates of all five points are different, and no three points lie on the same line. It is also assumed that if any point is shifted by a distance of 0.00001, the answer will remain the same.

Output

Output "1" if a star-shaped pentagon can be drawn, otherwise output "0" in one line.  

Sample Input and Output

Sample Input 1

1 4
7 4
2 1
4 6
6 1

Sample Output 1

1

Sample Input 2

1 4
4 6
2 1
7 4
6 1

Sample Output 2

0

---