Problem G: Building Water Ways

「水の帝国」と言われた古代ローマでは、都市や工場地に水を供給するために数多くの水路が建設され、今では古代の土木建設で最も偉大な業績のひとつと言われている。

この古代ローマ水道は当時の社会インフラとして人々の生活の質向上に大きく貢献したわけだが、古今東西、治水や水利に関する問題は興味深いものであり、水路建設に関するゲームも多く開発されている。

あなたの仕事は、与えられたマップにおいて水源から都市に水路を引くための最小のコストを求めるプログラムを書くことである。

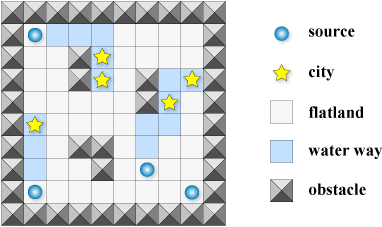
Figure 1

マップは Figure 1 に示すように、H × W のグリッドで表わされ、各升目は水源（source）、都市（city）、平地（flatland）、障害物（obstacle）のいづれかを示す。

各水源からは最大でも１本の水路を引くことしかできないが、水源が供給できる水の量に限りはない。そのため、１本の水路の長さには制限はなくその経路上の複数の都市に水を供給することができる。障害物がある場所に水路を引くことはできない。

あなたの目的は、最小のコストでマップ上の全ての都市の升目を水路の升目に染めることである。ここで、コストとはマップ上の水路の升目の総数である。Figure 1 では最小のコスト14で水路を建設している。

ただし、水路の建設にあたっては以下の条件を満たさなければならない：

• 水路は東西南北の方向に、最大で２つの水路と接する。
• 水源は東西南北の方向に、最大で１つの水路と接する。
• どの２つの水源も水路を通じて繋がらない。

Input

入力は複数のデータセットから構成される。各データセットは以下の形式で与えられる：

H W
H × W のマップ

H はマップの縦方向の升目の数、W は横方向の升目の数を示す。マップはH 行の文字列で与えられ、各行は W 文字から成る。各文字の意味は以下のようになる：

• 'P': 水源(source)
• '*': 都市(city)
• '.': 平地(flatland)
• '#': 障害物(obstacle)

入力の終わりは H = W = 0 であるデータセットによって示される。このデータセットに対する出力をしてはならない。

Output

各データセットについて、最小のコストを１行に出力せよ。

Constraints

• データセットの数は 60 を越えない。
• 3 ≤ H, W ≤ 10
• 1 ≤ 水源の数、都市の数 ≤ 8
• マップの回りは障害物で囲まれている。
• 水源同士は上下左右に隣接しない。
• 必ず解が存在する。

Sample Input

3 8
########
#P....*#
########
10 10
##########
#P.......#
#..#*....#
#..#*.#.*#
#.....#*.#
#*.......#
#..##....#
#...#.P..#
#P......P#
##########
0 0

Output for the Sample Input

5
14

---