Problem H: Hedro's Hexahedron

Dr. Hedro is astonished. According to his theory, we can make sludge that can dissolve almost everything on the earth. Now he's trying to produce the sludge to verify his theory.

The sludge is produced in a rectangular solid shaped tank whose size is N × N × 2. Let coordinate of two corner points of tank be (-N/2, -N/2, -1), (N/2, N/2, 1) as shown in Figure 1.

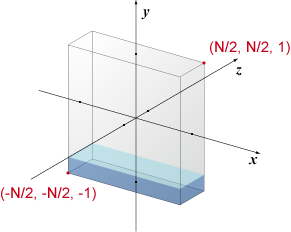
Figure 1

Doctor pours liquid that is ingredient of the sludge until height of the liquid becomes 1. Next, he get a lid on a tank and rotates slowly, without ruffling, with respect to z axis (Figure 2). After rotating enough long time, sludge is produced. Volume of liquid never changes through this operation.

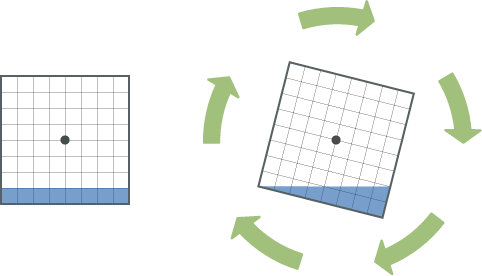
Figure 2

Needless to say, ordinary materials cannot be the tank. According to Doctor's theory, there is only one material that is not dissolved by the sludge on the earth. Doctor named it finaldefenceproblem (for short, FDP). To attach FDP tiles inside the tank allows to produce the sludge.

Since to produce FDP is very difficult, the size of FDP tiles are limited to 1 * 1. At first, doctor tried to cover entire the entire inside of the tank. However, it turned out that to make enough number FDP tiles that can cover completely is impossible because it takes too long time. Therefore, he decided to replace FDP tiles where an area the sludge touches is zero with those of ordinary materials. All tiles are very thin, so never affects height of the sludge.

How many number of FDP tiles does doctor need? He has imposed this tough problem on you, his helper.

Input

Input file contains several data sets. Each data set has one integer that describes N.

Input ends when N = 0. You should output nothing for this case.

Output

For each data set, print the number of tiles in a line.

Constraints

• Judge data consists of at most 150 datasets.
• 2 ≤ N ≤ 10¹²
• N is even number

Sample Input

2
4
0

Output for the Sample Input

24
64

---