Water Tank

伝次郎氏は理科の先生である． 彼は，水の流れに関する革新的な実験をするために水槽を注文していたのだが， 今日ちょうどその水槽が届いたところである．

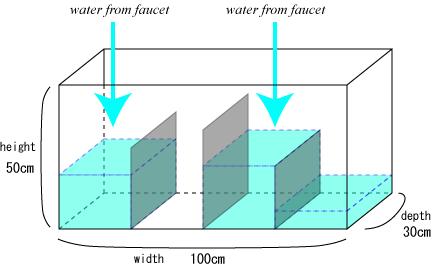Figure 1: The water tank

水槽は，幅100cm，高さ50cm，奥行き30cmの大きさである(Figure 1 参照)． 水槽の内部を区切るために，数枚の「区切り板」を水槽の側面と 平行に水槽の底に設置する． 区切り板の横幅はどれも水槽の奥行きである 30cm と等しい． 板の高さは水槽の側板の高さである 50cm よりは低い． また，板の高さは，板ごとにどれも異なっている． 区切り板は十分に薄いので，その厚さは無視できるものとする．

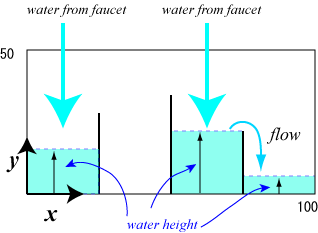Figure 2: The front view of the tank

水槽を正面から見ると Figure 2 のようになる．

水槽の上方にはいくつかの蛇口があり，実験開始と同時に蛇口を開いて 水を水槽へと注ぎ入れる．実験開始時に水槽は空である． あなたの仕事は，水槽内における水の流れを シミュレートするプログラムを書くことである．

Input

入力は，複数のデータセットからなる． D はデータセットの数を表す．

D
DataSet₁
DataSet₂
...
DataSet_D

各データセット (DataSet_d , ただし 1 <= d <= D) の形式は次の通りである．

N
B₁ H₁
B₂ H₂
...
B_N H_N
M
F₁ A₁
F₂ A₂
...
F_M A_M
L
P₁ T₁
P₂ T₂
...
P_L T_L

データセットの各行には1個または2個の整数が現れる．

N は彼が設置する区切り板の数を表す． B_i はi 番目の区切り板の x座標 (単位はcm) であり，H_i は その区切り板の高さ (単位はcm) を表す． ここで 1 <= i <= N である．

H_iはどれも異なっている． 以下の条件が成り立つと仮定してよい．

0 < N < 10 ,
0 < B₁ < B₂ < ... < B_N < 100 ,
0 < H₁ < 50 , 0 < H₂ < 50 , ..., 0 < H_N < 50.

M は水槽の上方に設置された水道の蛇口の数を表す． F_j はj番目の蛇口の x座標 (cm単位) であり， A_j はその蛇口から注ぎ込まれる水の流量 (cm³/秒)を表す．ただし 1 <= j <= Mである．

区切り板の真上に蛇口が来ることはない．すなわち F_j が B_i と一致することはない．

以下の条件が成り立つと仮定してよい．

0 < M <10 ,
0 < F₁ < F₂ < ... < F_M < 100 ,
0 < A₁ < 100, 0 < A₂ < 100, ... 0 < A_M < 100.

L は水の高さを測定する回数である． P_k は測定する場所の x 座標 (cm単位) であり， T_k は測定をする時刻 (実験開始からの経過時間，秒単位) である． ただし 1 <= k <= L である．

P_k が B_i と 一致することはない．

以下の条件が成り立つと仮定してよい．

0 < L < 10 ,
0 < P₁ < 100, 0 < P₂ < 100, ..., 0 < P_L < 100 ,
0 < T₁ < 1000000, 0 < T₂ < 1000000, ... , 0 < T_L < 1000000.

Output

各データセットに対して，実数を1個ずつ含む行を L行 出力しなさい． その実数は，指定された時刻 T_k における，指定された x 座標 P_k の 水の高さ(cm)を表していること．

解答の誤差は0.001を超えてはいけない． この条件を満たす限り， 小数点以下は何桁数字を表示してもかまわない．

水槽が満杯になって以後は，水槽の縁から水が溢れ出るので どのP_kの水の高さも水槽の高さと同じ，すなわち 50cm となる．

Sample Input

2
5
15 40
35 20
50 45
70 30
80 10
3
20 3
60 2
65 2
6
40 4100
25 7500
10 18000
90 7000
25 15000
25 22000
5
15 40
35 20
50 45
70 30
80 10
2
60 4
75 1
3
60 6000
75 6000
85 6000

Output for the Sample Input

0.666667
21.4286
36.6667
11.1111
40.0
50.0
30.0
13.3333
13.3333

---