Problem C: 六角沼の六角大蛇

六角沼は不思議な沼で，正六角形の窪みが整然と並ぶ．この沼をゆったり這いまわる六角大蛇(ろっかくおろち)は，環境に適応して正六角形の節が並んだ蛇．窪みひとつに節ひとつ．

六角大蛇が這うときには，いくつかの節を今ある窪みから隣の窪みに移す．体を分断するわけにはいかないので，動く前に隣同士だった節は，動いた後も隣同士でなくてはならない．ある節を動かすとき，すぐ隣の節はその動きを支えるので，一緒には動かせない．隣り合っていない節ならいくつでも同時に動かせる．

少し考えてみれば節を動せる先は，体の両端でせいぜい2箇所の窪み，体の中間の節ではせいぜい1箇所しかないのがわかるだろう．

たとえば，障害物がないときには六角大蛇は図C-1に左から右に示すように体をよじらせながら前進できる．8個の節のうち4個ずつを一度に動かし，4ステップかけてちょうど1コマ前進したことになる．もっともこいつらはヨコバイガラガラヘビみたいに，横に這う方が得意なのだが．

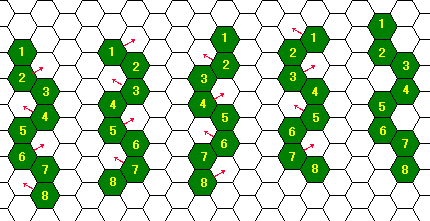
図 C-1: 前進する這い方

六角大蛇の皮膚はねばついていて，本来隣り合っている以外の節が隣の窪みに来ると (図C-2) 互いに癒着してしまい，大蛇はあえない最期を遂げる．もちろんひとつの窪みに節をふたつ入れることはできない．だからますます大蛇の動きはままならない．腹ペコでも，頭のすぐ隣の窪みにある食べ物にありつくのに苦労することもある．

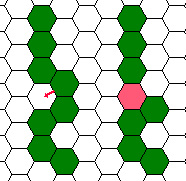
図 C-2: 死んでしまう場合

六角沼には，ところどころに岩がある．岩はそれぞれ窪みひとつの中に収まっていて，六角大蛇は岩とは癒着しないが，岩に乗り上げることはできない．岩のある窪みを避けるために大蛇の動きは制約されるが，やつらは沼の地形をよくわきまえていて，一番早く行ける経路を考えて通る．

あなたは科学者チームを率いて，この沼と大蛇の学術調査にあたることとなった．調査を完遂することも大事だが，人的損失は許されない．あなたの仕事は，いつまでに科学者のいる窪みに人食いの大蛇が頭（先頭の節）を動かしてこられるかを見積もることだ．頭以外の胴体の節にはまったく危険がなく，ハイテク非粘着スーツを着た科学者は大蛇の胴体と同じ窪みの中にいられる．

Input

入力はいくつかのデータセットが順に並んだもので，入力の終わりはゼロひとつだけの行で示される．データセット数が10を超えることはない．

各データセットの形式は以下のようなものである．

大蛇の節の数 (=n)
x₁ y₁
x₂ y₂
...
x_n y_n
沼の岩の個数 (=k)
u₁ v₁
u₂ v₂
...
u_k v_k
X Y

各データセットの先頭行には六角大蛇の持つ節の個数 n を表す整数が記されており，これは2以上で8を超えることはない．これに続く n 行には各々ふたつの整数 x および y がひとつの空白を区切りとして置かれ，大蛇の各節の座標を意味する．各行は，大蛇の頭から尻尾までの節の初期位置をこの順に示す．

データセットの次の行は沼の岩の個数 k を表し，これは100を超えない負でない整数である． これに続く k 行には，各々岩の位置を表すふたつの整数 u および v がある．

最後にふたつの整数 X と Y の行が来て，これは大蛇のゴール地点，すなわち科学者のいる位置を示す．最初はここには大蛇の頭はない．

座標を表す x, y, u, v, X, Y はいずれも −999999 以上 999999 以下である．同じ行のふたつの整数は空白ひとつで区切られる．入力には数字，マイナス記号，ふたつの整数を区切る空白以外の文字はない．位置を表す座標系は図 C-3 に示すようなものである．

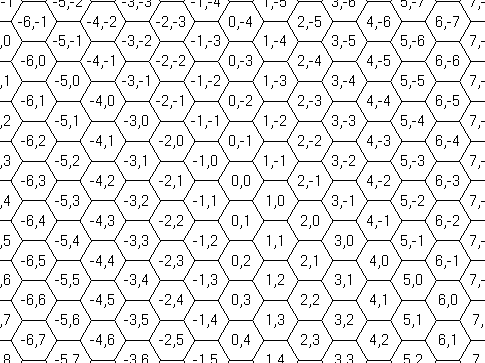
図 C-3: 座標系

Output

各データセットについて，大蛇がゴール地点までその頭を到達させるのに最小限必要なステップ数を表す十進数ひとつを含む1行を出力せよ．出力行には他のいかなる文字も含んではならない．

六角大蛇は20ステップ以内にゴールに到達できると仮定してよい．

Sample Input

3
2 -2
2 -1
1 0
1
0 2
0 0
4
2 -2
2 -1
2 0
3 0
2
1 -1
0 2
0 0
8
-6 0
-5 0
-4 0
-3 0
-2 0
-1 0
0 0
1 0
1
-1 1
0 0
6
2 -3
3 -3
3 -2
3 -1
3 0
2 1
3
1 -1
1 0
1 1
0 0
3
-8000 4996
-8000 4997
-8000 4998
2
-7999 4999
-8001 5000
-8000 5000
8
10 -8
9 -7
9 -6
9 -5
9 -4
9 -3
9 -2
9 -1
0
0 0
0

Output for the Sample Input

3
9
18
18
19
20

---