Problem D: カーリング 2.0

MM-21星でもオリンピック以来カーリングが流行している. しかし, そのルールは地球のものとはすこし異なっており, マス目状の氷の盤上で石を一つだけ使って行われる. スタート位置からゴール位置まで石を到達させる移動回数の少なさを競うのである.

図 D-1 に盤面の例を示す. 盤上のマス目には障害物が配置されていることがある. 盤面には, スタートとゴールという特別なマスが一つずつあり, そこには障害物はない. (スタートとゴールが一致することはない.) 滑りはじめた石は障害物がないかぎりどこまでも進んでいくので, ゴールに到達させるには, 障害物を利用していったん石を止め, あらためて滑らせてやる必要もあろう.

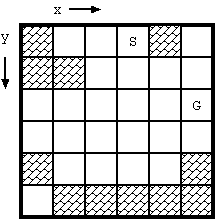
図 D-1: 盤面の例 (S: スタート, G: ゴール)

石の動きは以下の規則に従う:

ゲームの開始時に, 石はスタートで止まっている.
石の動きは x, y 方向に限る. ななめには動けない.
止まっている石は, 滑らせることによって動き出す. その時の方向は, すぐ次のマスに障害物がない方向ならどちらでもよい(図 D-2(a)).
動き出した石は, 次のいずれかが起こるまで, 同じ方向に動き続ける.
- 障害物にぶつかった場合(図 D-2(b), (c)).
  - 石は障害物の一つ手前のマスで止まる.
  - 障害物は消滅する.
- 盤外に出た場合.
  - 失敗でゲームは終わる.
- ゴールの上に来た場合.
  - そこで石は止まり, 成功でゲームは終わる.
1 回のゲーム中の滑らせる回数の最大は 10 である. この回数でゴールに石を到達させることができない場合, 失敗でゲームは終わる.

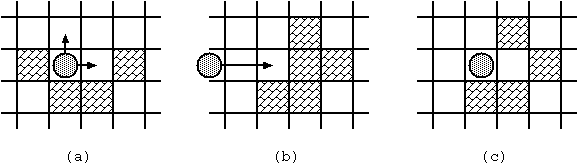
図 D-2: 石の動きの例

以上の条件のもとで, スタート位置にある石をゴール位置に到達させることができるか, できるなら最小何回滑らせればよいかを知りたい.

図 D-1 に示す初期配置では 4 回で石をスタート位置からゴール位置に動かすことができる. そのときの経路を図 D-3(a) に示す. なお, 石がゴールに到達した時点での盤面は図 D-3(b) のように変化している.

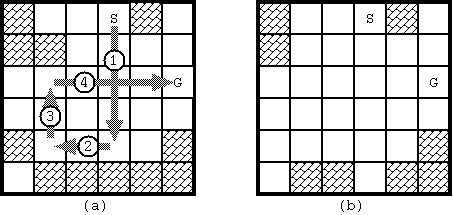
図 D-3: 図 D-1の解と終了時の盤面

Input

入力はデータセットの並びである. 入力の終わりは, 一つの空白で区切られた二つのゼロからなる行で示される. データセット数が100を超えることはない.

各データセットは次のような形式をしている:

盤の幅(=w) 盤の高さ(=h)
盤面の1行目
...
盤面のh行目

盤の幅と高さは次の条件を満たす: 2 <= w <= 20, 1 <= h <= 20.
盤面の各行には, w個の数字が空白一つをはさんで並んでいる. その数字は対応するマス目の状態を示している.

0 何もないマス

1 障害物

2 スタート位置

3 ゴール位置

図 D-1 に対応するデータセットの記述は以下のようになる:

6 6
1 0 0 2 1 0
1 1 0 0 0 0
0 0 0 0 0 3
0 0 0 0 0 0
1 0 0 0 0 1
0 1 1 1 1 1

Output

各データセットが指定する盤面について, スタート位置にある石をゴール位置に到達させるまでに滑らせる回数の最小値を, 十進の整数値でそれぞれ1行に出力せよ. そのような移動ができない場合には, -1 を出力せよ. 各出力行はこの数値以外の文字を含んではならない.

Sample Input

2 1
3 2
6 6
1 0 0 2 1 0
1 1 0 0 0 0
0 0 0 0 0 3
0 0 0 0 0 0
1 0 0 0 0 1
0 1 1 1 1 1
6 1
1 1 2 1 1 3
6 1
1 0 2 1 1 3
12 1
2 0 1 1 1 1 1 1 1 1 1 3
13 1
2 0 1 1 1 1 1 1 1 1 1 1 3
0 0

Output for the Sample Input

Source: https://onlinejudge.u-aizu.ac.jp/problems/1144

0	何もないマス
1	障害物
2	スタート位置
3	ゴール位置