Problem F 影の秘密

昔, 横浜近くの広場に何本かのまったく同じ大きさの円柱が垂直に立っていた (図 F-1). 日中, 太陽の動きに従って, 円柱の影は地面の上を動いた. 円柱はとても高かったので, その影は長かった. 図 F-2はその様子を真上から見たものである.

これらの円柱群の影の幅を最小あるいは最大にする太陽の方向が古くからの財宝に関する秘密を解く重要な鍵を与えると言われていた.

図 F-1: 円柱群

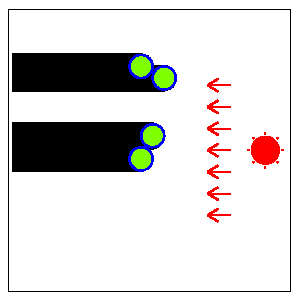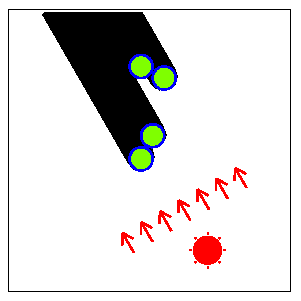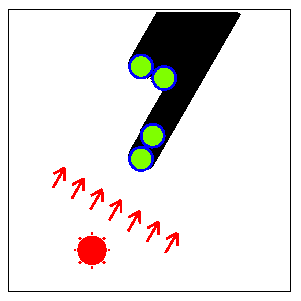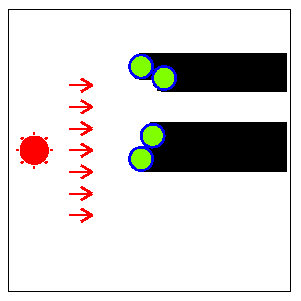
図 F-2: 円柱群(図 F-1)とその影を真上から見た図

一つの円柱だけを考えると, その影の幅は円柱底面の円の直径に等しい. しかし, ある円柱の影が別の円柱の影に重なることがあるので, 太陽の方向に従って, 影全体 (個々の円柱の影の合併) の幅は変化する.

図 F-2のような円柱の配置の場合, 影全体の幅が最小になるときの太陽の方向を図 F-3に示す.

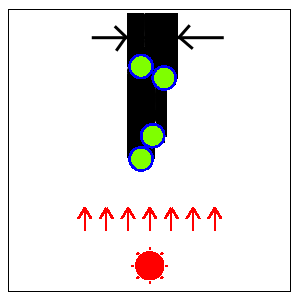
図 F-3: 影全体の幅が最小になる太陽の方向

影全体の幅が最大になるときの太陽の方向を図 F-4に示す. 影全体がいくつかの部分に分かれている場合(この例では2個), 影全体の幅はそれぞれの部分の影の幅の和である.

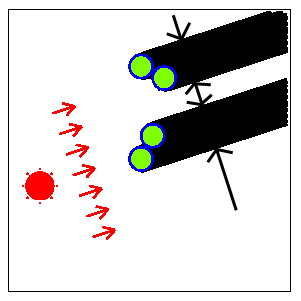
図 F-4: 影全体の幅が最大になる太陽の方向

太陽の方向は, 図 F-5に示される角度θで指定される. 東はθ=0, 南はθ=π/2, 西はθ=π である. 太陽は東(θ=0)から昇り, 西(θ=π)に沈むと仮定してよい.

あなたの仕事は, 円柱の配置が与えられたときに, その円柱群の影の幅が最小および最大になるときの太陽の方向 θ_min と θ_max を, それぞれ求めるプログラムを書くことである.

各円柱底面の円の中心の位置は, (x, y) 座標値で指定される. 東西方向をx軸, 南北方向をy軸とし, xの正の方向が東, yの正の方向が北である.

広場は平面であるとみなして良い.

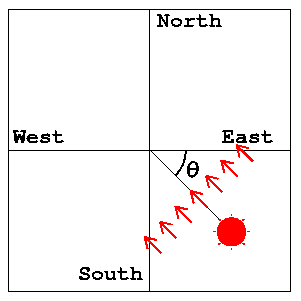
図 F-5: 太陽の方向を示す角度の定義

一般には, 円柱の配置に対して, 2個以上の θ_min や θ_max が存在することもある. しかし, ここでは θ_min および θ_max が 0<=θ_min<π, 0<=θ_max<π の範囲でそれぞれ唯一になるような円柱の配置だけを考える.

Input

入力は, 複数のデータセットの並び, および, 入力の終わりを示す 1行から成る. 入力の終わりを示す行は1個の0だけを含む.

各データセットは次のような形式をしている．

n
x₁ y₁
x₂ y₂
...
x_n y_n

n は広場にある円柱の本数である. 100以下の正の整数である.

x_k と y_k はk番目の円柱底面の円の中心の x座標とy座標である (k=1, ..., n). それらは30以下の正の整数である. それらは空白1個で区切られる.

なお, 各円柱底面の円の半径は 1 単位(直径は 2 単位) である. 円柱同士は接することはあっても重なることは無い.

たとえば, 次のデータセット

3
1 1
3 1
4 3

は図 F-6のような3本の円柱の配置を表す. このうち2本の円柱は互いに接している.

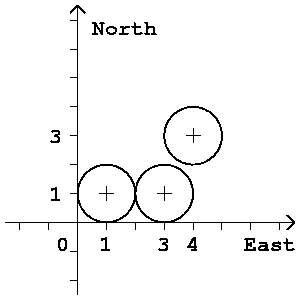
図 F-6: 3本の円柱の配置例

Output

各データセットについて，2行を出力せよ. 出力行の中に結果を表す数字以外のもの(たとえば空白)が含まれていてはならない.

1行目には, 影の幅を最小にする角度 θ_min を出力せよ. 2行目には, 影の幅を最大にする角度 θ_max を出力せよ. 出力される角度θは 0以上π以下の区間([0,π]と略記する)に含まれなければならない. ε=0.0000000001 (=10^-10) として, εを超える誤差が無いようにすること.

ただし, 正解の角度θの値が[0,ε]の区間に属するときには, [0,θ+ε] および [π+θ-ε,π]の区間に属する近似値を正解とみなす. また, 正解の角度θの値が[π-ε,π]に属するときには, [0,θ+ε-π]および[θ-ε,π]の区間に属する近似値を正解とみなす.

上記の誤差の範囲内であれば, 小数点以下何個の数字を出力してもよい.

Sample Input

Output for the Sample Input

2.553590050042226
0.982793723247329
1.570796326794896
2.819842099193151
1.325817663668032
2.094395102393196
2.777613697080149
0.588002603547568

Source: https://onlinejudge.u-aizu.ac.jp/problems/1146