Problem E: 大玉転がし

ACM 大学では毎年 7 月に運動会が開かれるが， そのハイライトとなる競技は大玉転がしである． この大玉転がしではグラウンド上にひかれた直線状のコースに沿って大玉を転がす． グラウンドには複数の直方体ブロックが障害物として置かれていて動かすことができない． ブロックに大玉がぶつからないように， かつ大玉の底の点がコースの線から離れないように転がさなければならない．

競技をおもしろくするために，大玉をなるべく大きなものにすることになった． 上の条件を満たすような転がし方が可能な大玉の半径の最大値を求めるプログラムを作成しなさい．

大玉は完全な球，グラウンドは平面とする． ブロックの形は直方体である．ブロックの底面の四辺はグラウンド上にあり， X, Y 軸のいずれかと平行になっている． コースは，始点から終点までの線分として与えられる． 大玉の底の点が始点に接している状態からスタートし， 終点に接している状態でゴールするものとする．

なお，大玉とブロックの位置関係は，図 E-1 (a), (b) のようになる可能性がある．

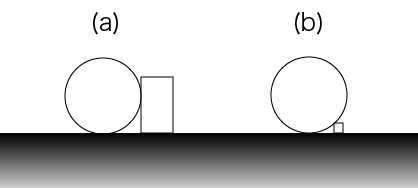
図 E-1: 大玉とブロックの位置関係

Input

入力は，いくつかのデータセットからなる． 各データセットは以下の形式で与えられる．

N
sx sy ex ey
minx₁ miny₁ maxx₁ maxy₁ h₁
minx₂ miny₂ maxx₂ maxy₂ h₂
...
minx_N miny_N maxx_N maxy_N h_N

データセットの最初の行はブロックの数を表す整数 N (1 ≤ N ≤ 50) からなる．次の行は空白ひとつで区切られたよっつの整数からなり， 始点の座標 (sx, sy)，終点の座標 (ex, ey) を表す． 続く N 行はそれぞれ空白ひとつで区切られたいつつの整数からなる． 1 行がひとつのブロックに対応し，ブロックの底面の 2 頂点 (minx, miny), (maxx, maxy) と高さ h を表す． 整数 sx, sy, ex, ey, minx, miny, maxx, maxy, h は以下の条件を満たすものとする．

-10000 ≤ sx, sy, ex, ey ≤ 10000
-10000 ≤ minx_i < maxx_i ≤ 10000
-10000 ≤ miny_i < maxy_i ≤ 10000
1 ≤ h_i ≤ 1000

入力の終わりはゼロひとつの行で示される．

Output

入力データセットごとに大玉の半径の最大値を表す実数を 1 行出力せよ．なお， 与えられたデータセットに対して，半径の最大値が 1000 を超えることはないと仮定してよい．また，コースの線の上にブロックがある場合の， 大玉の半径の最大値は 0 とする．出力する値は 0.001 以下の誤差を含んでいても構わない．値は小数点以下何桁表示しても構わない．

Sample Input

2
-40 -40 100 30
-100 -100 -50 -30 1
30 -70 90 -30 10
2
-4 -4 10 3
-10 -10 -5 -3 1
3 -7 9 -3 1
2
-40 -40 100 30
-100 -100 -50 -30 3
30 -70 90 -30 10
2
-400 -400 1000 300
-800 -800 -500 -300 7
300 -700 900 -300 20
3
20 70 150 70
0 0 50 50 4
40 100 60 120 8
130 80 200 200 1
3
20 70 150 70
0 0 50 50 4
40 100 60 120 10
130 80 200 200 1
3
20 70 150 70
0 0 50 50 10
40 100 60 120 10
130 80 200 200 3
1
2 4 8 8
0 0 10 10 1
1
1 4 9 9
2 2 7 7 1
0

Output for the Sample Input

30
1
18.16666666667
717.7857142857
50.5
50
18.16666666667
0
0

---