Dr. Fukuoka has invented fancy panels. Each panel has a square shape of a unit size and has one of the six colors, namely, yellow, pink, red, purple, green and blue. The panel has two remarkable properties. One property is that, when two or more panels with the same color are placed adjacently, their touching edges melt a little and they are fused each other. The fused panels are united into a polygonally shaped panel. The other property is that the color of a panel can be changed to one of six colors by giving an electrical shock. The resulting color can be controlled by its waveform. The electrical shock to an already united panel changes the color of the whole to a specified single color.

Since he wants to investigate the strength with respect to the color and the size of a united panel compared to unit panels, he tries to unite panels into a polygonal panel with a specified color.

Figure C-1: panels and their initial colors

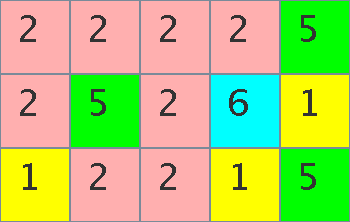
Since many panels are simultaneously synthesized and generated on a base plate through some complex chemical processes, the fabricated panels are randomly colored and they are arranged in a rectangular shape on the base plate (Figure C-1). Note that the two purple (color 4) panels in Figure C-1 are already united at the initial state since they are adjacent to each other.

Installing electrodes to a panel, and changing its color several times by giving electrical shocks according to an appropriate sequence for a specified target color, he can make a united panel merge the adjacent panels to unite them step by step and can obtain a larger panel with the target color. Unfortunately, panels will be broken when they are struck by the sixth electrical shock. That is, he can change the color of a panel or a united panel only five times.

Let us consider a case where the panel at the upper left corner of the panel configuration (Figure C-1) is attached with the electrodes. First, changing the color of the panel from yellow to blue, the two adjacent panels are fused into a united panel (Figure C-2).

Figure C-2: Change of the color of the panel at the upper left corner, from yellow (color 1) to blue (color 6).

Second, changing the color of the upper left united panel from blue to red, a united red panel that consists of three unit panels is newly formed (Figure C-3). Then, changing the color of the united panel from red to purple, panels are united again to form a united panel of five unit panels (Figure C-4).

Figure C-3: Change of the color of the panel at the upper left corner, from blue (color 6) to red (color 3).

Figure C-4: Change of the color of the panel at the upper left corner, from red (color 3) to purple (color 4).

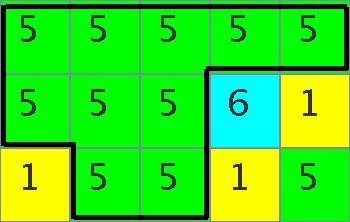
Furthermore, through making a pink united panel in Figure C-5 by changing the color from purple to pink, then, the green united panel in Figure C-6 is obtained by changing the color from pink to green. The green united panel consists of ten unit panels.

Figure C-5: Change of the color of the panel at the upper left corner, from purple (color 4) to pink (color 2).

Figure C-6: Change of the color of the panel at the upper left corner, from pink (color 2) to green (color 5).

In order to check the strength of united panels with various sizes and colors, he needs to unite as many panels as possible with the target color. Your job is to write a program that finds a sequence to change the colors five times in order to get the largest united panel with the target color. Note that the electrodes are fixed to the panel at the upper left corner.

The input consists of multiple datasets, each being in the following format.

h w c
p_1,1 p_1,2 ... p_1,w
p_2,1 p_2,2 ... p_2,w
...
p_h,1 p_h,2 ... p_h,w

h and w are positive integers no more than 8 that represent the height and the width of the given rectangle. c is a positive integer no more than 6 that represents the target color of the finally united panel. p_i,j is a positive integer no more than 6 that represents the initial color of the panel at the position (i, j).

The end of the input is indicated by a line that consists of three zeros separated by single spaces.

For each dataset, output the largest possible number of unit panels in the united panel at the upper left corner with the target color after five times of color changes of the panel at the upper left corner. No extra characters should occur in the output.

3 5 5
1 6 3 2 5
2 5 4 6 1
1 2 4 1 5
4 5 6
1 5 6 1 2
1 4 6 3 2
1 5 2 3 2
1 1 2 3 2
1 1 5
1
1 8 6
1 2 3 4 5 1 2 3
8 1 1
1
2
3
4
5
1
2
3
8 8 6
5 2 5 2 6 5 4 2
4 2 2 2 5 2 2 2
4 4 4 2 5 2 2 2
6 4 5 2 2 2 6 6
6 6 5 5 2 2 6 6
6 2 5 4 2 2 6 6
2 4 4 4 6 2 2 6
2 2 2 5 5 2 2 2
8 8 2
3 3 5 4 1 6 2 3
2 3 6 4 3 6 2 2
4 1 6 6 6 4 4 4
2 5 3 6 3 6 3 5
3 1 3 4 1 5 6 3
1 6 6 3 5 1 5 3
2 4 2 2 2 6 5 3
4 1 3 6 1 5 5 4
0 0 0

10
18
1
5
6
64
33