In Northern Kyushu, you are running a company which rents watchdogs in response to the customers' order. The distinguishing point of your service is that you also install fences to enhance the performance of watchdogs.

The dog is put on a leash, which is tied up to a peg. You are installing fences at the border of the dog's reach, so that strangers approaching the fence are taken care of by your dog.

There may be a rectangular building near the dog; the dog cannot enter the building, but can go around it as long as the length of the leash permits, as in Figure F-1. You do not need fences along the building's wall.

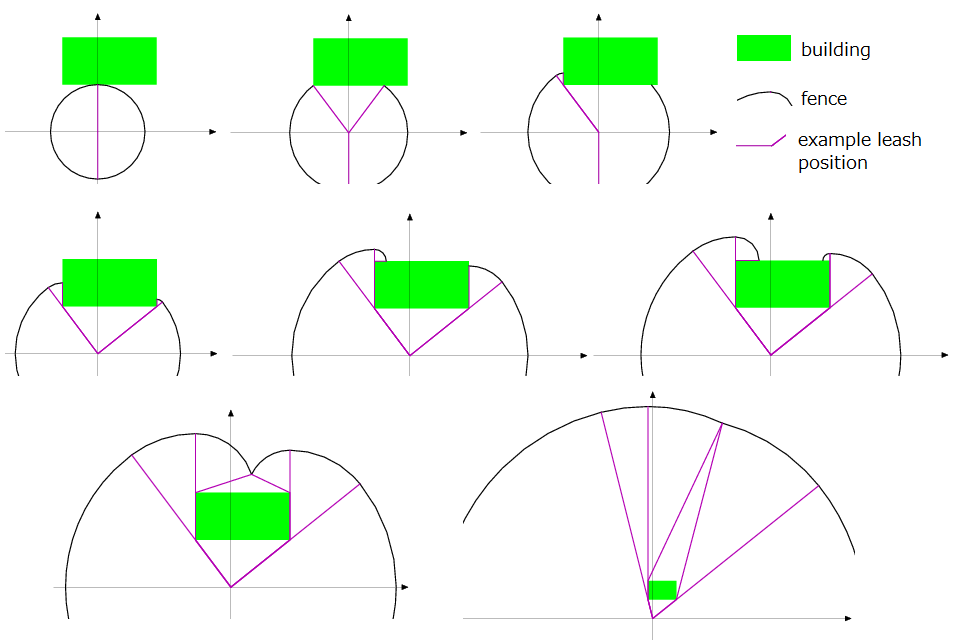
Figure F-1: Example fence layouts (some parts of the fences are omitted.)

Given the length of the leash and the position and the size of the building, your program should calculate the length of the fence.

The input consists of multiple datasets each consisting of five integers in a line of the following format.

len x₁ y₁ x₂ y₂

len indicates the length of the leash. x₁, y₁, x₂ and y₂ indicate the size and position of the building in that a point with coordinate (x,y) such that x₁ < x <x₂ and y₁ < y < y₂ is contained in the building. This means that the building's walls are parallel to either the X-axis or Y-axis. The peg is located on the origin.

You may assume that 0 < len ≤ 100, −100 ≤ x₁ < x₂ ≤ 100 and −100 ≤ y₁ < y₂ ≤ 100. You may also assume that the peg is located apart from the building (that is, neither inside nor on the border of the building).

The end of the input is indicated by a line containing five zeros.

For each dataset, output the total length of the fences as a single fractional number in a line. There may not be any other characters in the output. The output should not contain an error greater than 0.00001.

3 3 0 6 5
5 3 0 6 5
6 3 0 6 5
7 3 0 6 5
9 3 0 6 5
10 3 0 6 5
12 3 0 6 5
100 3 0 6 5
4 -3 4 5 8
5 -3 4 5 8
6 -3 4 5 8
64 -30 40 50 50
7 -3 4 5 8
10 -3 4 5 8
11 -3 4 5 8
14 -3 4 5 8
35 -3 4 5 8
100 -3 4 5 8
10 5 9 12 12
13 5 9 12 12
15 5 9 12 12
18 5 9 12 12
19 5 9 12 12
20 5 9 12 12
21 5 9 12 12
100 5 9 12 12
100 -5 1 -3 5
100 0 1 100 2
100 -1 99 100 100
10 -1 1 1 2
84 1 -77 5 -42
27 -12 -7 3 -4
0 0 0 0 0

18.84955592
26.77945045
31.69103413
39.54501577
55.51851918
63.83954229
75.38181750
628.05343108
25.13274123
24.98091545
29.43519428
318.90944272
35.02723766
55.44758990
64.23914179
89.33649537
219.11188064
627.48648370
62.83185307
76.33420961
88.61222855
112.17417345
121.59895141
126.16196589
132.25443447
628.23333565
628.18890261
626.17695473
613.16456638
62.61625003
527.84509612
168.07337509