Watchdog Corporation
In Northern Kyushu, you are running a company which rents watchdogs in response to the customers' order. The distinguishing point of your service is that you also install fences to enhance the performance of watchdogs.
The dog is put on a leash, which is tied up to a peg. You are installing fences at the border of the dog's reach, so that strangers approaching the fence are taken care of by your dog.
There may be a rectangular building near the dog; the dog cannot enter the building, but can go around it as long as the length of the leash permits, as in Figure F-1. You do not need fences along the building's wall.
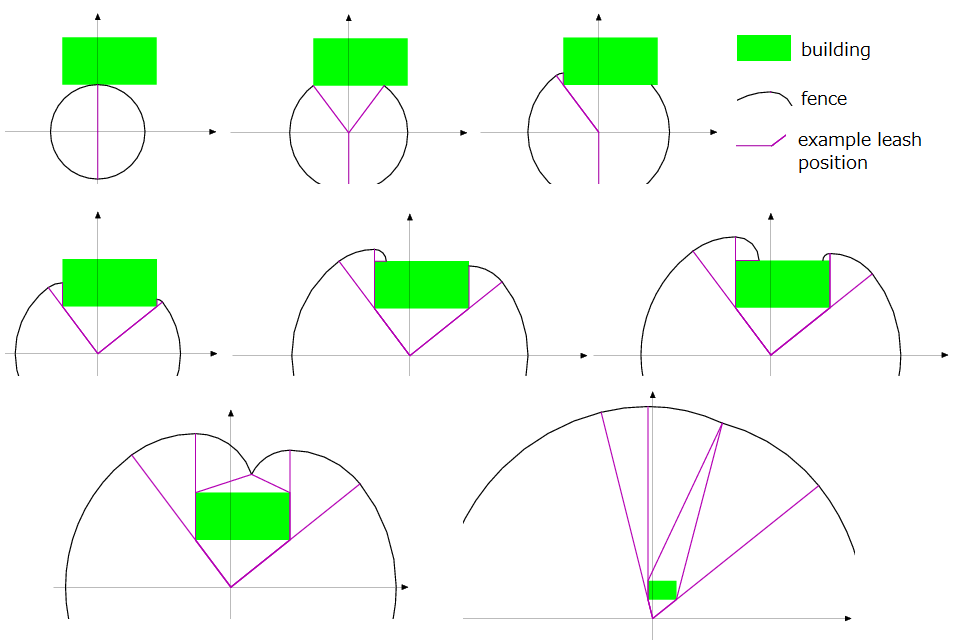
Figure F-1: Example fence layouts (some parts of the fences are omitted.)
Given the length of the leash and the position and the size of the building, your program should calculate the length of the fence.
Input
The input consists of multiple datasets each consisting of five integers in a line of the following format.
len x1 y1 x2 y2
len indicates the length of the leash. x1, y1, x2 and y2 indicate the size and position of the building in that a point with coordinate (x,y) such that x1 < x <x2 and y1 < y < y2 is contained in the building. This means that the building's walls are parallel to either the X-axis or Y-axis. The peg is located on the origin.
You may assume that 0 < len ≤ 100, −100 ≤ x1 < x2 ≤ 100 and −100 ≤ y1 < y2 ≤ 100. You may also assume that the peg is located apart from the building (that is, neither inside nor on the border of the building).
The end of the input is indicated by a line containing five zeros.
Output
For each dataset, output the total length of the fences as a single fractional number in a line. There may not be any other characters in the output. The output should not contain an error greater than 0.00001.
Sample Input
3 3 0 6 5 5 3 0 6 5 6 3 0 6 5 7 3 0 6 5 9 3 0 6 5 10 3 0 6 5 12 3 0 6 5 100 3 0 6 5 4 -3 4 5 8 5 -3 4 5 8 6 -3 4 5 8 64 -30 40 50 50 7 -3 4 5 8 10 -3 4 5 8 11 -3 4 5 8 14 -3 4 5 8 35 -3 4 5 8 100 -3 4 5 8 10 5 9 12 12 13 5 9 12 12 15 5 9 12 12 18 5 9 12 12 19 5 9 12 12 20 5 9 12 12 21 5 9 12 12 100 5 9 12 12 100 -5 1 -3 5 100 0 1 100 2 100 -1 99 100 100 10 -1 1 1 2 84 1 -77 5 -42 27 -12 -7 3 -4 0 0 0 0 0
Output for the Sample Input
18.84955592 26.77945045 31.69103413 39.54501577 55.51851918 63.83954229 75.38181750 628.05343108 25.13274123 24.98091545 29.43519428 318.90944272 35.02723766 55.44758990 64.23914179 89.33649537 219.11188064 627.48648370 62.83185307 76.33420961 88.61222855 112.17417345 121.59895141 126.16196589 132.25443447 628.23333565 628.18890261 626.17695473 613.16456638 62.61625003 527.84509612 168.07337509