偏りのあるサイコロ
確率的アルゴリズムの大家であるランダム教授は現在,偏りのあるサイコロの実験を行っている.実験というのは,平面の上方の決まった位置から次々にサイコロを落とすものである.サイコロは平面またはすでにそこにあるサイコロの上に回転せずに落ち,さらに転がり落ちることもある.結果としては,積み上がった山の状態,具体的には上から見たときにどの目がいくつ見えるかを記録する.すべてのサイコロは同じ大きさで,数の振り方はすべて図C-1のようになっている.
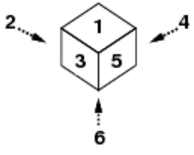
図C-1: サイコロの面の配置
ここで用いるサイコロは非常に特殊な性質を持っている.
(1)通常のサイコロは4方向に転がることができるが,ここで用いるサイコロは4,5,6の面の方向にしか転がらない(1,2,3の面の方向には転がれない).図C-2に示す状況では,ここで用いるサイコロ(our die)は2方向にしか転がらない.
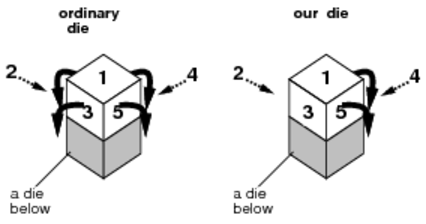
図C-2: 通常のサイコロと偏りのあるサイコロ
(2)サイコロが転がるのは,転がった後に落ちる時のみである.この様子を図C-3に示す.転がりうる方向が複数ある場合は,最も大きな目の面の方向に転がる.
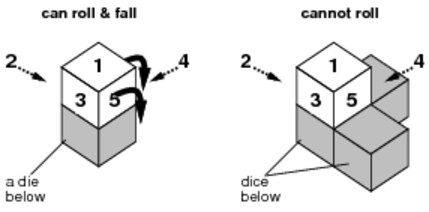
図C-3: サイコロは落ちられる時だけ転がれる
(3)転がる場合には,図C-4の[B],[C]のように,ちょうど90度回転した後,まっすぐ下に落ち,平面か他のサイコロの上に着地する.
(4)サイコロは一度転がり落ちた後も,(1)〜(3)の規則に従い繰り返し転がり落ちる.
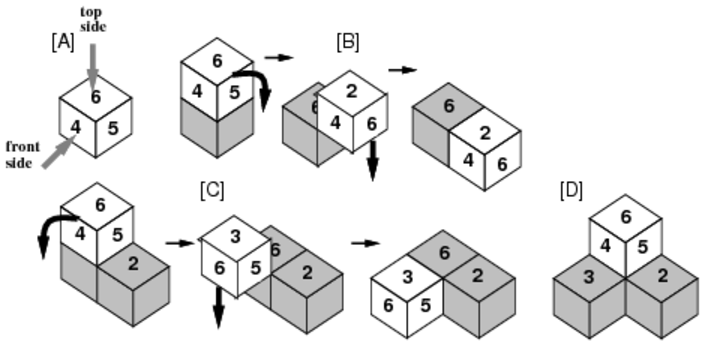
図C-4: 偏りのあるサイコロの積みあがり方の例
たとえば,同じ向き(上面が6,前面が4)で4つのサイコロを落下させた場合,図C-4のように山ができる.
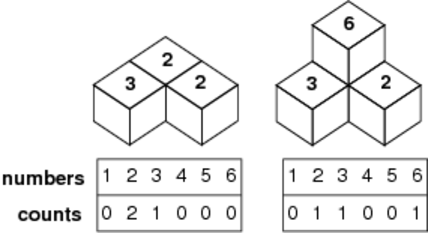
図C-5: 記録の例
山が完成したら,1から6までの面が上からいくつ見えるかを数えて記録する.たとえば図C-5の左の場合は記録は「0 2 1 0 0 0」となり,右の場合は「0 1 1 0 0 1」となる.
Input
入力は複数のデータセットからなり,各データセットは次の形式で表される.
n
t1 f1
t2 f2
...
tn fn
ここでn (1 ≤ n ≤ 100) は整数であり,落とすサイコロの個数である.ti とfi (1 ≤ ti, fi ≤ 6) は1つの空白で区切られた整数であり,i番目のサイコロから手を放す瞬間の上面と前面の目である.
入力の終わりは1つのゼロだけからなる行によって示される.
Output
各データセットごとに,6個の整数を1個の空白文字で区切って出力せよ.それぞれの整数は1〜6それぞれの目が上方向から何個見えるかを表す.出力にはこれら以外の文字があってはならない.
Sample Input
4 6 4 6 4 6 4 6 4 2 5 3 5 3 8 4 2 4 2 4 2 4 2 4 2 4 2 4 2 4 2 6 4 6 1 5 2 3 5 3 2 4 4 2 0
Output for the Sample Input
0 1 1 0 0 1 1 0 0 0 1 0 1 2 2 1 0 0 2 3 0 0 0 0