整長方形

高さhと幅wがともに整数である長方形を考えよう．そのような長方形を整長方形と呼ぶ．以下，この問題では横長の整長方形，すなわち w > h である整長方形のみを考える．

横長整長方形の大小関係を次のように定めよう．

1. 対角線の長さが短いほうが小さい．
2. 対角線の長さが同じならば，高さの低いほうが小さい．

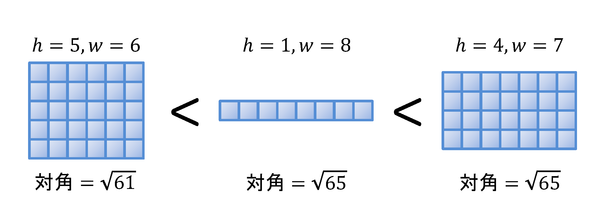
与えられた横長整長方形に対し，それより大きい最小の横長整長方形を求めよ．

Input

入力全体は複数のデータセットからなる．データセットの数は100以下である． 各データセットはひとつの横長整長方形を記述しており，その高さhと幅wがひとつの空白で区切られた以下のような1行である．

h w

各データセットについて，hとw（>h）は，ともに，1以上100以下の整数である．

入力の終わりは，ひとつの空白で区切られたふたつの0から成る行によって示される．

Output

各データセットに対し，それに記述されている横長整長方形より大きい最小の横長整長方形の高さhと幅w (> h) とを，整数でひとつの空白文字で区切って1行に出力せよ．出力にはこれら以外の文字があってはならない．

なお，この問題の入力で与えられる横長整長方形に対しては，それより大きい最小の横長整長方形の高さと幅はともに150を超えないことが分かっている．

また，この問題では横長整長方形の大小を決めるために対角線の長さの大小比較を用いているが，これは対角線の長さの二乗の大小比較を用いても同じことである．対角線の長さの二乗の大小比較を用いることにより，浮動小数点計算の誤差によって生じうるトラブルを避けることができる．

Sample Input

1 2
1 3
2 3
1 4
2 4
5 6
1 8
4 7
98 100
99 100
0 0

Output for the Sample Input

1 3
2 3
1 4
2 4
3 4
1 8
4 7
2 8
3 140
89 109

---