つながれた風船
地面上に風船があり,地面上の1つ以上の杭とロープでつながれている. 各ロープは,風船と杭をつなぐのに十分な長さがある. ロープ同士は交差していない. 図 E-1 は,そのような状況を示したものである.
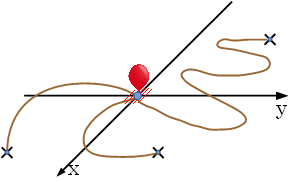
図E-1: 地面上にある風船とロープ
今,風船が飛びはじめた. あなたの仕事は,風船がロープの接続を維持したまま, どこまで高く飛ぶことができるか答えることである. 杭の位置は,固定されている. ロープの長さと,杭の位置は与えられる. また,ロープに重さはなく,どの方向に引っ張られたとしても, 一直線になりうると考えてよい. 図E-2は,図E-1の状態から風船が飛びはじめた時に, 風船が一番高くあがった位置を表している.
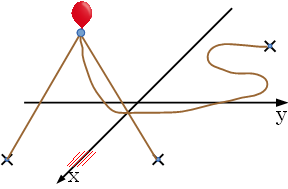
図E-2: 風船が一番高くあがった位置
Input
入力は複数のデータセットからなり, 各データセットは次の形式で表される.
n
x1 y1 l1
...
xn yn ln
データセットの最初の行は,ロープの本数を表す整数 n (1 ≤ n ≤ 10) のみからなる. 続く n 行のそれぞれは,空白文字 1 個で区切られた 3 個の整数 xi, yi, li からなる. Pi = (xi, yi) は, i 番目のロープをつなぐ杭の位置を表し, li はそのロープの長さを表す. −100 ≤ xi ≤ 100, −100 ≤ yi ≤ 100, 1 ≤ li ≤ 300 であると仮定してよい. また,風船は,最初,地面上の (0, 0) に位置している. 風船および杭のサイズは無視してよい.
PiとPj (i ≠ j) は異なる位置を表すものとする. また,Piから (0, 0) への距離は,li−1 以下であると仮定してよい. このため,風船は少なくとも高さ1まで飛ぶことができる.
図 E-1 と E-2 は,後に示す Sample Input 中の最初のデータセットに対応している.
入力の終わりは,ゼロを一つだけ含む行で表される.
Output
各データセットに対して,風船が飛ぶことのできる最大の高さを 1 行で出力せよ. 答えには 0.00001 を超える誤差があってはいけない. それ以外の余計な文字を出力してはならない.
Sample Input
3 10 10 20 10 -10 20 -10 10 120 1 10 10 16 2 10 10 20 10 -10 20 2 100 0 101 -90 0 91 2 0 0 53 30 40 102 3 10 10 20 10 -10 20 -10 -10 20 3 1 5 13 5 -3 13 -3 -3 13 3 98 97 168 -82 -80 193 -99 -96 211 4 90 -100 160 -80 -80 150 90 80 150 80 80 245 4 85 -90 290 -80 -80 220 -85 90 145 85 90 170 5 0 0 4 3 0 5 -3 0 5 0 3 5 0 -3 5 10 95 -93 260 -86 96 211 91 90 177 -81 -80 124 -91 91 144 97 94 165 -90 -86 194 89 85 167 -93 -80 222 92 -84 218 0
Output for the Sample Input
17.3205081 16.0000000 17.3205081 13.8011200 53.0000000 14.1421356 12.0000000 128.3928757 94.1879092 131.1240816 4.0000000 72.2251798