バンパイア

C氏はバンパイアである．太陽の光を直接浴びると灰になってしまうのだが，昨夜， 不死者と死人のプログラマー同好会(ICPC)に参加していたら，帰宅が夜明けに近い時間になってしまった． 幸いなことに，C氏の自宅周辺には背の高いビルが多く，太陽の光がビルにさえぎられている間は安全に動き回ることができる． いま太陽の上端が地平線にかかったところだが，C氏が安全に棺桶に入るまでにあと何秒の猶予があるだろうか?

簡単のため，東の空をx 軸が水平，y 軸が垂直方向の2次元 x-y 平面で表し，建物のシルエットはこの平面上の長方形， 太陽は円で近似するものとする．

x 軸が地平線を表す．時刻をt で表し，現在の時刻をt=0とする．太陽は半径 r で，時刻 t=0 における中心は (0, -r) にあり，x-y平面上を 毎秒 (0, 1) の等速直線運動を しているものとする．

太陽(境界線を含む)の全体が，シルエット(境界線を含む)および地平線以下の領域(y ≤ 0)の和集合に含まれていれば，太陽の光はさえぎられている．

太陽の光がさえぎられている最後の瞬間の時刻を計算するプログラムを書け．

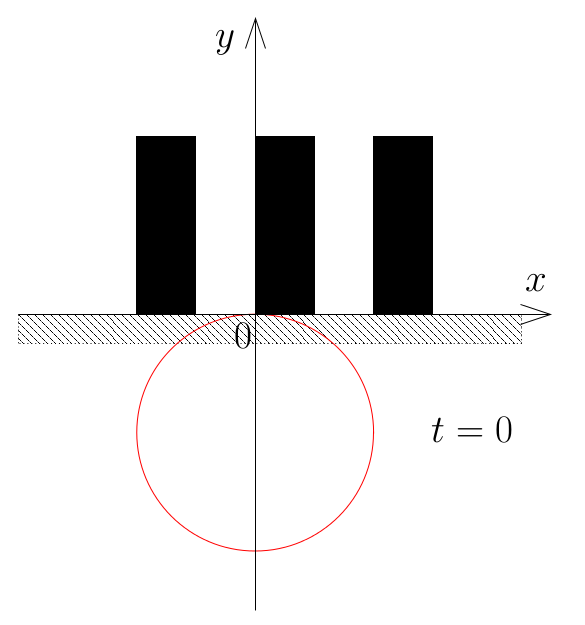
次の図は，後に示す Sample Input 中の最初のデータセットに対応するシルエットの配置と 太陽の光がさえぎられている最後の瞬間 (t=0) を示す． このように，時刻 t=0 が太陽の光がさえぎられている最後の瞬間であることもありうる．

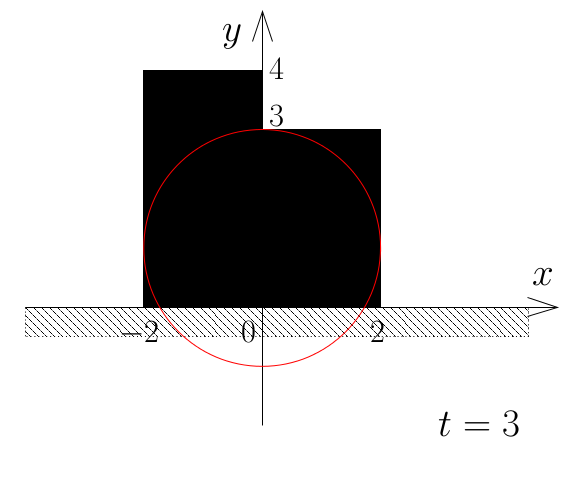
シルエット同士が辺で接する場合も，隙間は無く太陽の光はさえぎられる． 下の図は，Sample Input の 2番目のデータセットに対応するシルエットの配置と， 太陽の光がさえぎられている最後の瞬間 (t=3) を示す． 太陽の半径が 2で， -2 ≤ x ≤ 0 に高さ 4，0 ≤ x ≤ 2 に高さ 3 の2つのシルエットが与えられた例である．

Input

入力は複数のデータセットからなる．各データセットの最初の行は， 空白で区切られた2つの整数 r と n からなる． r は太陽の半径を表し，n は建物のシルエットの個数を表す． (1 ≤ r ≤ 20, 0 ≤ n ≤ 20)

続く n行のそれぞれは，空白で区切られた 3つの整数 x_li， x_ri， h_i (1 ≤ i ≤ n) からなる．

この 3つの整数は，建物のシルエットの長方形を指定する．シルエットの長方 形は地平線に平行で，左右の辺はx = x_li と x = x_ri に一致し，上辺は y = h_i に，下辺は地平線に一致している． (-20 ≤ x_li < x_ri ≤ 20, 0 < h_i ≤ 20)

入力の終わりは空白で区切られた 2つのゼロからなる行で表される．

こうして与えられる建物のシルエットは重なっているかもしれないので注意すること．

Output

各データセットに対し，太陽の光がさえぎられている最後の瞬間の時刻tを1行に出力せよ． 答えには 0.001 を越える誤差があってはならない． それ以外の余計な文字を出力してはならない．

Sample Input

2 3
-2 -1 3
0 1 3
2 3 3
2 2
-2 0 4
0 2 3
2 6
-3 3 1
-2 3 2
-1 3 3
0 3 4
1 3 5
2 3 6
2 6
-3 3 1
-3 2 2
-3 1 3
-3 0 4
-3 -1 5
-3 -2 6
0 0

Output for the Sample Input

0.0000
3.0000
2.2679
2.2679

---