論理式圧縮機
あなたは論理式の意味を保ったまま短くする圧縮機の作成を依頼された.
論理式の文法は, 0 1 a b c d - ^ * ( ) を終端記号,<E> を開始記号とし,次の生成規則を持つ.
<E> ::= 0 | 1 | a | b | c | d | -<E> | (<E>^<E>) | (<E>*<E>)
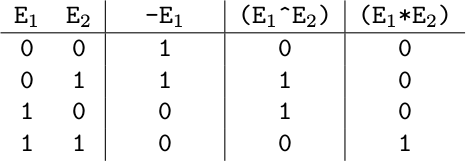
ここで,a, b, c, d は, 値として 0 または 1 を持つ論理変数である. 各演算子は下の表に示すように評価する. すなわち,- は否定 (NOT) を, ^ は排他的論理和 (XOR) を, * は論理積 (AND) をそれぞれ表す.
4 変数がどんな値を持っていても与えられた式と同じ評価結果になる式のうちで, 最も短い式の長さを求めるプログラムを書きなさい.
例えば,Sample Input の最初にある式 0 は, これ以上短くすることができない.したがって,最短の長さは 1 である.
Sample Input の 2 番目の (a*(1*b)) は, (a*b) や (b*a) と必ず同じ計算結果になり, これらが最短である.したがって,出力は 5 になる.
Input
入力は複数のデータセットからなる. データセットは 1 行であり,上述の文法に従う式一つが書かれている. 式の長さは 16 文字以下である.
入力の終わりは ‘.’ (ピリオド) 一つのみからなる行で表される. 入力に含まれるデータセットの数は高々 200 である.
Output
各データセットについて, 変数の値の全組み合わせに対して,同じ値を計算する最も短い式の長さを表す整数一つからなる行を出力せよ.
Sample Input
0 (a*(1*b)) (1^a) (-(-a*-b)*a) (a^(b^(c^d))) .
Output for the Sample Input
1 5 2 1 13