Origami, or the art of folding paper
Master Grus is a famous origami (paper folding) artist, who is enthusiastic about exploring the possibility of origami art. For future creation, he is now planning fundamental experiments to establish the general theory of origami.
One rectangular piece of paper is used in each of his experiments. He folds it horizontally and/or vertically several times and then punches through holes in the folded paper.
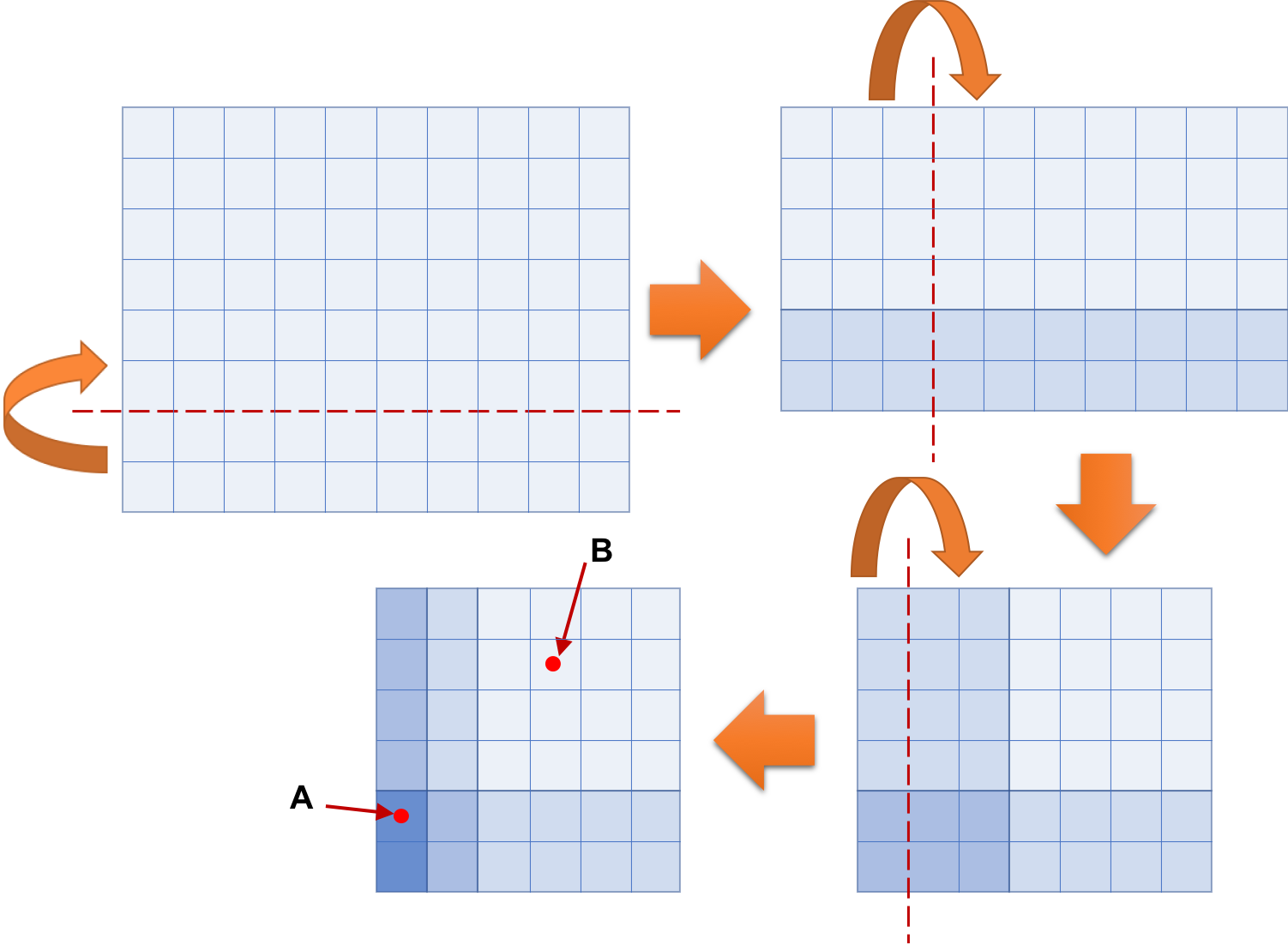
The following figure illustrates the folding process of a simple experiment, which corresponds to the third dataset of the Sample Input below. Folding the 10 × 8 rectangular piece of paper shown at top left three times results in the 6 × 6 square shape shown at bottom left. In the figure, dashed lines indicate the locations to fold the paper and round arrows indicate the directions of folding. Grid lines are shown as solid lines to tell the sizes of rectangular shapes and the exact locations of folding. Color densities represent the numbers of overlapping layers. Punching through holes at A and B in the folded paper makes nine holes in the paper, eight at A and another at B.
Your mission in this problem is to write a computer program to count the number of holes in the paper, given the information on a rectangular piece of paper and folding and punching instructions.
Input
The input consists of at most 1000 datasets, each in the following format.
n m t p
d1 c1
...
dt ct
x1 y1
...
xp yp
n and m are the width and the height, respectively, of a rectangular piece of paper. They are positive integers at most 32. t and p are the numbers of folding and punching instructions, respectively. They are positive integers at most 20. The pair of di and ci gives the i-th folding instruction as follows:
- di is either 1 or 2.
- ci is a positive integer.
- If di is 1, the left-hand side of the vertical folding line that passes at ci right to the left boundary is folded onto the right-hand side.
- If di is 2, the lower side of the horizontal folding line that passes at ci above the lower boundary is folded onto the upper side.
The end of the input is indicated by a line containing four zeros.
Output
For each dataset, output p lines, the i-th of which contains the number of holes punched in the paper by the i-th punching instruction.
Sample Input
2 1 1 1 1 1 0 0 1 3 2 1 2 1 2 1 0 0 10 8 3 2 2 2 1 3 1 1 0 1 3 4 3 3 3 2 1 2 2 1 1 1 0 1 0 0 0 0 0 0
Output for the Sample Input
2 3 8 1 3 6